
分析 根据所给的直线3x-4y-5=0,得到直线的斜率时$\frac{3}{4}$,直线的斜率是倾斜角的正切,得到tanα=$\frac{3}{4}$,α∈[0,π],根据倾斜角的范围和正切的反三角函数的值域确定结果.
解答 解:∵直线3x-4y-5=0,
∴直线的斜率时$\frac{3}{4}$,
直线的斜率是倾斜角的正切,
∴tanα=$\frac{3}{4}$,α∈[0,π],
∴α=arctan$\frac{3}{4}$,
故答案为:arctan$\frac{3}{4}$.
点评 本题考查反三角函数的应用及直线的倾斜角与斜率的关系,本题解题的关键是理解反三角函数的值域和倾斜角的范围,本题是一个基础题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{CD}$ | B. | $\overrightarrow{DC}$ | C. | $\overrightarrow{AD}$ | D. | $\overrightarrow{CB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
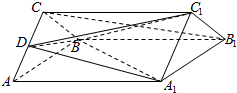 如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D
如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$,+∞) | B. | (1,$\sqrt{3}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线为l1、l2.过椭圆C的右焦点F作直线l,使l丄l1.设直线l与椭圆C的两个交点由上至下依次为A,B,直线l与直线l2交于P点.
如图,已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线为l1、l2.过椭圆C的右焦点F作直线l,使l丄l1.设直线l与椭圆C的两个交点由上至下依次为A,B,直线l与直线l2交于P点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com