
| A. | 7个 | B. | 252个 | C. | 210个 | D. | 35个 |
分析 运用数列相邻两项差的值,可能够取值的情况分类讨论,转化为排列组合问题求解.
解答 解:∵数列{bn}共有8项且满足b1=2014,b8=2015,
∴b8-b1=b8-b7+b7-b6+b6-b5+b5-b4+b4-b3+b3-b2+b2-b1=1,
bn+1-bn∈{-1,$\frac{1}{3}$,1}(其中n=1,2,…,7),共有7对差,
可能bn+1-bn=-1,或bn+1-bn=$\frac{1}{3}$,或bn+1-bn=1.
设-1有x个,$\frac{1}{3}$有y个,1有7-x-y个,
则x(-1)+$\frac{y}{3}$+1×(7-x-y)=1,
即6x+2y=18,x,y∈[0,7]的整数,
可判断;x=1,y=6;x=2,y=3;x=3,y=0,三组符合
所以共有数列${C}_{7}^{1}+{C}_{7}^{3}{C}_{4}^{2}{C}_{2}^{2}+{C}_{7}^{3}{C}_{4}^{4}$=7+210+35=252.
故选:B.
点评 本题考查了方程的解转化为组合问题等基础知识与基本技能方法,考查了推理能力,转化能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}+2$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}+2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
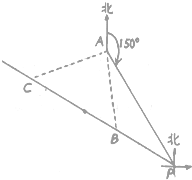 海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.
海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com