
【题目】已知函数![]()
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)证明: ![]() 在
在![]() 上为增函数;
上为增函数;
(3)证明:方程![]() =0没有负数根。
=0没有负数根。
 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() ),x∈R的图象,只需将函数y=sin2x,x∈R的图象上所有的点( )
),x∈R的图象,只需将函数y=sin2x,x∈R的图象上所有的点( )
A.向左平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向右平行移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程序框图如图所示,现输入如下四个函数:f(x)= ![]() ,f(x)=x4 , f(x)=2x , f(x)=x﹣
,f(x)=x4 , f(x)=2x , f(x)=x﹣ ![]() ,则可以输出的函数是( )
,则可以输出的函数是( ) 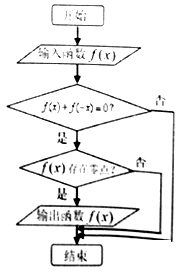
A.f(x)= ![]()
B.f(x)=x4
C.f(x)=2x
D.f(x)=x﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务蓬勃发展. 2016年“618”期间,某网购平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对该网购平台的商品和服务的评价系统. 从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的![]() 列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(Ⅱ) 若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满意的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:![]()
![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的一个顶点为A(0,1),离心率为
=1(a>b>0)的一个顶点为A(0,1),离心率为 ![]() ,过点B(0,﹣2)及左焦点F1的直线交椭圆于C,D两点,右焦点设为F2 .
,过点B(0,﹣2)及左焦点F1的直线交椭圆于C,D两点,右焦点设为F2 .
(1)求椭圆的方程;
(2)求△CDF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知BC边上的高所在直线的方程为x﹣2y+1=0,∠A平分线所在直线的方程为y=0,若点B的坐标为(1,2), (Ⅰ)求直线BC的方程;
(Ⅱ)求点C的坐标.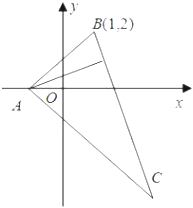
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
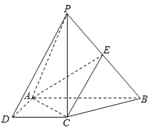
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com