
已知两条不重合的直线m、n和两个不重合的平面α、β,有下列命题:
①若m⊥n,m⊥α,则n∥α;
②若m⊥α,n⊥β,m∥n,则α∥β;
③若m、n是两条异面直线,m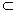 α,n
α,n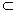 β,m∥β,n∥α,则α∥β;
β,m∥β,n∥α,则α∥β;
④若α⊥β,α∩β=m,n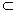 β,n⊥m,则n⊥α.
β,n⊥m,则n⊥α.
其中正确命题的个数是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
科目:高中数学 来源: 题型:
函数f(x)=sin(2x+φ) 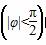 的图像向左平移
的图像向左平移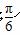 个单位后所得函数图像的解析式是奇函数,则函数f(x)在
个单位后所得函数图像的解析式是奇函数,则函数f(x)在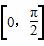 上的最小值为( )
上的最小值为( )
A.-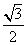 B.-
B.-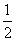
C.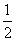 D.
D.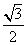
查看答案和解析>>
科目:高中数学 来源: 题型:
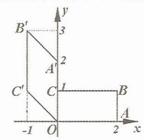
如图,矩形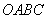 在变换
在变换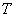 的作用下变成了平行四边形
的作用下变成了平行四边形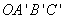 ,变换
,变换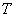 所对应的矩阵为
所对应的矩阵为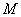 ,矩阵
,矩阵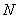 是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵。 (Ⅰ)求
是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵。 (Ⅰ)求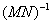 ;(Ⅱ)判断矩阵
;(Ⅱ)判断矩阵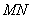 是否存在特征值。
是否存在特征值。
查看答案和解析>>
科目:高中数学 来源: 题型:
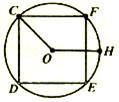
如图,CDEF是以圆O为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在扇形OCFH内”(点H将劣弧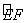 二等分),则事件A发生的概率P(A)= 。
二等分),则事件A发生的概率P(A)= 。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数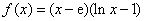
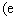 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求曲线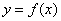 在
在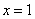 处的切线方程;
处的切线方程;
(Ⅱ)若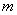 是
是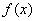 的一个极值点,且点
的一个极值点,且点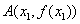 ,
,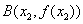 满足条件:
满足条件:
 .
.
(ⅰ)求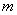 的值;
的值;
(ⅱ)求证:点 ,
, ,
,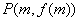 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com