
设集合I={1,2,3,4,5}.选择I的两个非空子集A和B,求使B中最小的数大于A中最大的数的不同选择方法有多少种?
49
解析解:当A中最大的数为1时,B可以是{2,3,4,5}的非空子集,有24-1=15(种)选择方法;
当A中最大的数为2时,A可以是{2}或{1,2},B可以是{3,4,5}的非空子集,有2×(23-1)=14种选择方法;
当A中最大的数为3时,A可以是{3,},{1,3},{2,3}或{1,2,3},B可以是{4,5}的非空子集,有4×(22-1)=12(种)选择方法;
当A中最大的数为4时,A可以是{4},{1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,,3,4}或{1,2,3,4},B可以是{5},有8×1=8(种)选择方法.
所以满足条件的非空子集共有15+14+12+8=49(种)不同的选择方法.


科目:高中数学 来源: 题型:解答题
已知非空有限实数集S的所有非空子集依次记为S1,S2,S3, ,集合Sk中所有元素的平均
值记为bk.将所有bk组成数组T:b1,b2,b3, ,数组T中所有数的平均值记为m(T).
(1)若S={1,2},求m(T);
(2)若S={a1,a2, ,an}(n∈N*,n≥2),求m(T).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1)在(1+x)n的展开式中,若第3项与第6项系数相等,则n等于多少?
(2)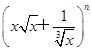 的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.
的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com