
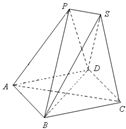
 如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为
如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为 .
. 分别作出两个正三棱锥的高PN、SM,连接AC交BD于O,连接OP、OS
分别作出两个正三棱锥的高PN、SM,连接AC交BD于O,连接OP、OS ,OM=
,OM=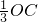 ∴MN=
∴MN=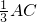
 AB=6
AB=6 ?MN=
?MN=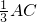 =2
=2

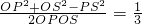


 ,AN=
,AN= ,
, =
=
 =
= ×
×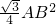 ×
× =
=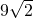
 =
=
 ,从而PS=2
,从而PS=2 ,在等腰三角形PSO中利用余弦定理结合二面角P-BD-S的余弦值为
,在等腰三角形PSO中利用余弦定理结合二面角P-BD-S的余弦值为 计算出PO长,再在Rt三角形POB中求出PB长,得到△PBD、△PBA都是等腰直角三角形,从而结合线面垂直的判定得到PB⊥平面PAD;
计算出PO长,再在Rt三角形POB中求出PB长,得到△PBD、△PBA都是等腰直角三角形,从而结合线面垂直的判定得到PB⊥平面PAD; ,从而得到正三棱锥P-ABD的体积为
,从而得到正三棱锥P-ABD的体积为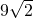 ,最终可得多面体SPABC的体积.
,最终可得多面体SPABC的体积.

科目:高中数学 来源: 题型:解答题
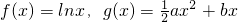 .
.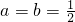 时,求函数h(x)=f(x)-g(x)的单调区间;
时,求函数h(x)=f(x)-g(x)的单调区间;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 成立,那么一定有
成立,那么一定有查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 是否属于M,并说明理由;
是否属于M,并说明理由;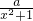 属于M,求实数a的取值范围.
属于M,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com