
 ,
, ,
, ,其中0<φ<π,且函数
,其中0<φ<π,且函数 的图象过点
的图象过点 .
. 个单位,然后将得到函数图象上各点的横坐标变为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在[0,
个单位,然后将得到函数图象上各点的横坐标变为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在[0, ]上的最大值和最小值.
]上的最大值和最小值. 和
和 的值,进而求得f(x)=cos(2x-φ),再把点
的值,进而求得f(x)=cos(2x-φ),再把点 代入函数的解析式可得φ 的值.
代入函数的解析式可得φ 的值. ),根据y=Asin(ωx+∅)的图象变换规律求得g(x)=cos(x-
),根据y=Asin(ωx+∅)的图象变换规律求得g(x)=cos(x- ),再由x∈[0,
),再由x∈[0, ],利用余弦函数的定义域和值域求得函数g(x)的最大值和最小值.
],利用余弦函数的定义域和值域求得函数g(x)的最大值和最小值. =(cosφ,sinφ)•(cosx,sinx)=cosφcosx+sinφsinx=cos(φ-x),
=(cosφ,sinφ)•(cosx,sinx)=cosφcosx+sinφsinx=cos(φ-x), =(cosx,sinx)•(sinφ-cosφ)=sinφcosx-cosφsinx=sin(φ-x),
=(cosx,sinx)•(sinφ-cosφ)=sinφcosx-cosφsinx=sin(φ-x), =cos(φ-x)cosx+sin(φ-x)sinx=cos(φ-x-x)=cos(2x-φ).
=cos(φ-x)cosx+sin(φ-x)sinx=cos(φ-x-x)=cos(2x-φ). 代入可得 cos(
代入可得 cos( -φ)=1.
-φ)=1. .
. ),图象向左平移
),图象向左平移 个单位,
个单位, )-
)- ]=cos(2x-
]=cos(2x- )的图象;然后将得到函数图象上各点的横坐标变为原来的2倍,
)的图象;然后将得到函数图象上各点的横坐标变为原来的2倍, )的图象,
)的图象, ).
). ],可得 x-
],可得 x- ∈[-
∈[- ,
, ],
], =0时,函数g(x)=cos(x-
=0时,函数g(x)=cos(x- ) 取得最大值为1,
) 取得最大值为1, =
= 时,函数g(x)=cos(x-
时,函数g(x)=cos(x- ) 取得最小值为
) 取得最小值为  .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| AB |
| AP |
| 2 |
| 2 |
| 7π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AB |
| AP |
| 2 |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AB |
| AP |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2013届度广东省高二上学期11月月考理科数学试卷 题型:解答题
(本题满分12分)已知对任意的平面向量,把 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角,得到向量
角,得到向量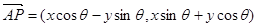 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 角得到点P
角得到点P
①已知平面内的点A(1,2),B ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线 ,求原来曲线C的方程.
,求原来曲线C的方程.
查看答案和解析>>
科目:高中数学 来源:2014届安徽省铜陵市高一3月月考数学试卷 题型:解答题
(本小题满分13分)
已知对任意平面向量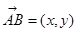 ,把
,把 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角得到向量
角得到向量 ,叫做把点
,叫做把点 绕点
绕点 逆时针方向旋转角得到点
逆时针方向旋转角得到点 。
。
(1)已知平面内点 ,点
,点 。把点
。把点 绕点
绕点 沿逆时针旋转
沿逆时针旋转 后得到点
后得到点 ,求点
,求点 的坐标;
的坐标;
(2)设平面内直线 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转 后得到的点组成的直线方程是
后得到的点组成的直线方程是 ,求原来的直线
,求原来的直线 方程。
方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com