Question

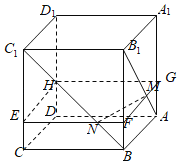
【题目】在正方体ABCD-A1B1C1D1中，点M、N分别在AB1、BC1上，且AM=AB1，BN=BC1，则下列结论：①AA1⊥MN；②A1C1// MN；③MN//平面A1B1C1D1；④B1D1⊥MN，其中，

正确命题的个数是（ ）

A.1B.2C.3D.4

Answer 1

【答案】B

【解析】

由题意在四条棱A1A，B1B，C1C，D1D上分别取点G，F，E，H四点，使AGA1A，BFB1B，CEC1C，DHD1D，得到平面GFEH，则点M，N在与平面A1B1C1D1平行的平面GFEH中．利用线面垂直的性质判断①正确；利用平行公理判断②错误；利用面面平行的性质判断③正确；利用面面平行以及线线垂直的性质判断④错误．

在正方体ABCD﹣A1B1C1D1的四条棱A1A，B1B，C1C，D1D上分别取点G，F，E，H四点，

使AGA1A，BFB1B，CEC1C，DHD1D，连接GF，FE，EH，HG，

∵点M、N分别在AB1、BC1上，且AMAB1，BNBC1，

∴M在线段GF上，N点在线段FE上．且四边形GFEH为正方形，平面GFEH∥平面A1B1C1D1，

∵AA1⊥平面A1B1C1D1，∴AA1⊥平面GFEH，

∵MN平面GFEH，∴AA1⊥MN，故①正确；

∵A1C1∥GE，而GE与MN不平行，∴A1C1与MN不平行，故②错误；

∵平面GFEH∥平面A1B1C1D1，MN平面GFEH，∴MN∥平面A1B1C1D1，故③正确；

∵B1D1∥FH，FH平面GFEH，MN平面GFEH，且MN与FH不垂直，∴B1D1与MN不垂直，故④错误．

∴正确命题只有①③．

故选：B．