
(10分). 函数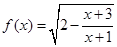 的定义域为集合A,函数
的定义域为集合A,函数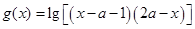 的定义域为集合B.
的定义域为集合B.
(1)求A; (2)若B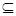 A,求实数
A,求实数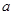 的取值范围。
的取值范围。
(1)A:x<-1或x≥1;(2)a>1或a≤-2或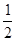 ≤a<1;
≤a<1;
【解析】
试题分析:(1)首先利用分式不等式得到集合A。
(2)同时利用对数真数大于零得到集合B,然后根据集合A,B的包含关系,借助于数轴法得到参数a的范围。
解:(1)A:x<-1或x≥1; --------------------------------3分
(2)B:(x-a-1)(x-2a)<0
∵φ≠B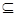 A,∴①
A,∴①
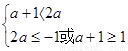 ∴a>1
------------------------6分
∴a>1
------------------------6分
或②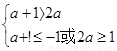 ∴a≤-2或
∴a≤-2或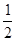 ≤a<1;
---------------------------8分
≤a<1;
---------------------------8分
∴a>1或a≤-2或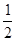 ≤a<1;
-------------10分
≤a<1;
-------------10分
考点:本题主要考查了集合的求解以及子集的概念的运用。
点评:解决该试题的关键是理解分式不等式的求解,以及对数函数定义域的求解,利用结合的包含关系,结合数轴法得到结论。


科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2014届广东省东莞市高二下学期期末考试理科数学试卷(A)(解析版) 题型:选择题
函数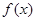 的定义域为R,
的定义域为R,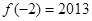 ,对任意
,对任意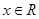 ,都有
,都有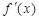 <
<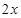 成立,则不等式
成立,则不等式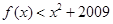 的解集为( )
的解集为( )
A. (-2,2)
B. (-2,+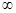 ) C. (-
) C. (-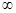 ,-2)
D. (-
,-2)
D. (-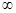 ,+
,+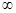 )
)
查看答案和解析>>
科目:高中数学 来源:2014届海南琼海嘉积中学高二上教学监测(三)理科数学试卷(解析版) 题型:选择题
函数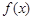 的定义域为
的定义域为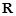 ,
,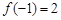 ,对任意
,对任意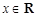 ,
,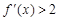 ,则
,则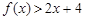 的解集为:
的解集为:
A.(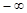 ,+
,+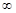 ) B.(
) B.(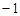 ,1)
,1)
C.(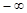 ,
,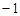 ) D.(
) D.(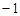 ,+
,+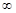 )
)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省齐齐哈尔市高三三模文科数学试卷(解析版) 题型:选择题
函数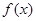 的定义域为
的定义域为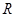 ,
,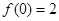 ,对
,对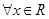 ,有
,有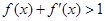 ,则不等式
,则不等式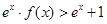 的解集为( )
的解集为( )
A.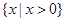 B.
B.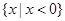
C.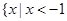 或
或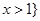 D.
D.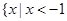 或
或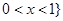
查看答案和解析>>
科目:高中数学 来源:2012届安徽省高三第一学期期中文科数学试卷 题型:解答题
已知函数 的定义域为
的定义域为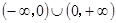 ,且满足条件:①
,且满足条件:① ,②
,② ③当
③当 .
.
(1)求证:函数 为偶函数;
为偶函数;
(2)讨论函数 的单调性;
的单调性;
(3)求不等式 的解集
的解集
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com