
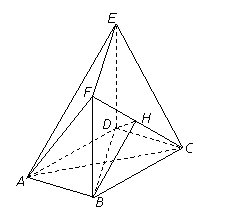
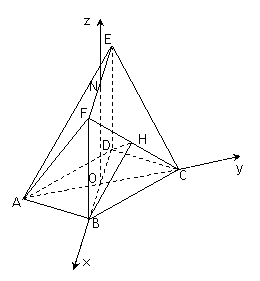
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,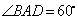 ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3, H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3, H是CF的中点.
 (Ⅰ)求证:AC⊥平面BDEF;
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求直线DH与平面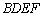 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角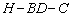 的大小.
的大小.
(Ⅰ)证明:因为四边形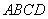 是菱形,
是菱形,
所以 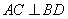 .
.
因为平面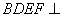 平面
平面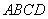 ,且四边形
,且四边形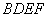 是矩形,
是矩形,
所以 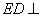 平面
平面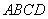 ,
,
又因为 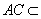 平面
平面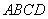 ,
,
所以 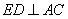 .
.
因为 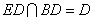 ,
,
所以 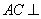 平面
平面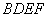 .
.
(Ⅱ)解:设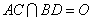 ,取
,取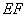 的中点
的中点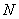 ,连接
,连接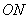 ,
,
因为四边形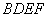 是矩形,
是矩形,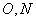 分别为
分别为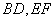 的中点,
的中点,
所以 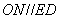 ,
,
又因为 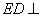 平面
平面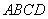 ,所以
,所以  平面
平面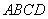 ,
,
由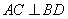 ,得
,得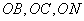 两两垂直.
两两垂直.
所以以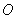 为原点,
为原点,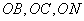 所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.
所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.
 因为底面
因为底面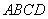 是边长为2的菱形,
是边长为2的菱形,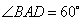 ,
,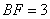 ,
,
所以 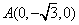 ,
,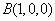 ,
,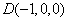 ,
,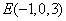 ,
,
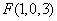 ,
,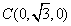 ,
, .
.
因为 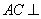 平面
平面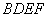 ,
,
所以平面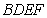 的法向量
的法向量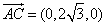 .
.
设直线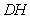 与平面
与平面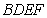 所成角为
所成角为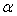 ,
,
由 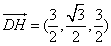 ,
,
得 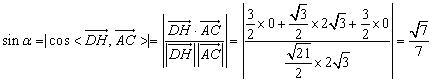 ,
,
所以直线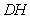 与平面
与平面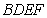 所成角的正弦值为
所成角的正弦值为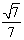 .
.
(Ⅲ)解:由(Ⅱ),得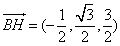 ,
,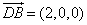 .
.
设平面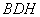 的法向量为
的法向量为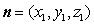 ,
,
所以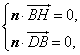
即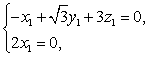
令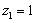 ,得
,得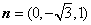 .
.
由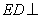 平面
平面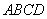 ,得平面
,得平面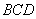 的法向量为
的法向量为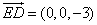 ,
,
则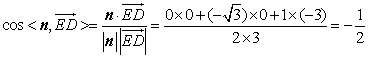 .
.
由图可知二面角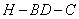 为锐角,
为锐角,
所以二面角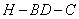 的大小为
的大小为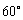 .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
已知圆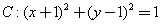 与x轴切于A点,与y轴切于B点,设劣弧
与x轴切于A点,与y轴切于B点,设劣弧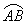 的中点为M,则过点M的圆C的切线方程是( )
的中点为M,则过点M的圆C的切线方程是( )
(A)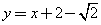
(B)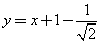
(C)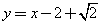
(D)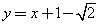
|
查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |