
| A. | (-1,+∞) | B. | (-∞,-1) | C. | [-1,+∞) | D. | (-∞,-1) |
分析 利用参数分离法将不等式进行转化,利用换元法转化为一元二次函数,判断对称轴求出函数在区间上最值即可得到结论.
解答 解:若x∈[1,2],y∈[2,3]时,$\frac{a{x}^{2}+2{y}^{2}}{xy}$-1>0恒成立,
则ax2+2y2>xy,
即ax2>xy-2y2,
即a>$\frac{xy-2{y}^{2}}{{x}^{2}}$=$\frac{y}{x}$-2($\frac{y}{x}$)2,
设t=$\frac{y}{x}$,则a>t-2t2,
∵x∈[1,2],y∈[2,3],
∴$\frac{1}{x}$∈[$\frac{1}{2}$,1],则t=$\frac{y}{x}$∈[1,3],
设f(t)=t-2t2,t∈[1,3],
则f(t)=t-2t2,的对称轴为t=$\frac{1}{4}$,
则函数在[1,3]上为减函数,
∴当t=1时,函数取得最大值f(1)=1-2=-1,
则a>-1,
即实数a的取值范围是(-1,+∞),
故选:A.
点评 本题主要考查不等式恒成立问题,利用参数分离法结合换元法进行转化,结合一元二次函数的最值性质是解决本题的关键.考查学生的转化能力.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
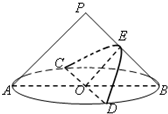 如图,在底面半径和高均为2的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为2的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\frac{{\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增加了$\frac{1}{2(k+1)}$ | B. | 增加了$\frac{1}{2k+1}$+$\frac{1}{2k+2}$ | ||
| C. | 增加了$\frac{1}{2k+1}$+$\frac{1}{2k+2}$,但减少了$\frac{1}{k+1}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | R | C. | B | D. | A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
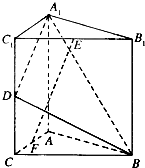 如图,在直三棱柱ABC-A1B1C1中,C1C=CB=CA=2,AC⊥CB,D,E分别为棱C1C,B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,C1C=CB=CA=2,AC⊥CB,D,E分别为棱C1C,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,|x0|+x${\;}_{0}^{2}$≥0 | B. | ?x0∈R,|x0|+x${\;}_{0}^{2}$<0 | ||
| C. | ?x∈R,|x|+x2<0 | D. | ?x∈R,|x|+x2≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
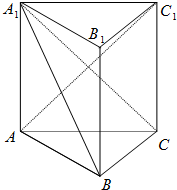 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com