
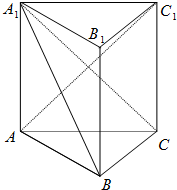
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.分析 (I)先证BC⊥平面ACC1A1得BC⊥AC1,由四边形ACC1A1为正方形得出AC1⊥A1C,故而AC1⊥平面A1BC,于是AC1⊥A1B;
(II)由AC1⊥平面A1BC可知∠ABO是直线AB与平面A1BC所成的角,设BC=a,利用勾股定理求出OA,OB即可得出tan∠ABO.
解答 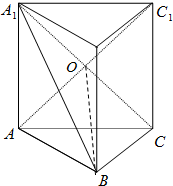 证明(Ⅰ)∵CC1⊥平面ABC,BC?平面ABC,
证明(Ⅰ)∵CC1⊥平面ABC,BC?平面ABC,
∴CC1⊥BC
又∠ACB=90°,即BC⊥AC,又AC∩CC1=C,
∴BC⊥平面A1C1CA,又AC1?平面A1C1CA,
∴AC1⊥BC.
∵AA1=AC,∴四边形A1C1CA为正方形,
∴AC1⊥A1C,又AC1∩BC=C,
∴AC1⊥平面A1BC,又A1B?平面A1BC,
∴AC1⊥A1B.
解(Ⅱ)设AC1∩A1C=O,连接BO.
由(Ⅰ)得AC1⊥平面A1BC,
∴∠ABO是直线AB与平面A1BC所成的角.
设BC=a,则AA1=AC=2a,∴$AO=\frac{1}{2}A{C_1}=\sqrt{2}a$,$BO=\sqrt{{a^2}+2{a^2}}=\sqrt{3}a$,
在Rt△ABO中,$tan∠ABO=\frac{AO}{BO}=\frac{{\sqrt{6}}}{3}$,
∴直线AB与平面A1BC所成角的正切值为$\frac{{\sqrt{6}}}{3}$.
点评 本题考查了线面垂直的判断与性质,线面角的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1) | C. | [-1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
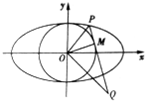 在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点A($\sqrt{6}$,1),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.
在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点A($\sqrt{6}$,1),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
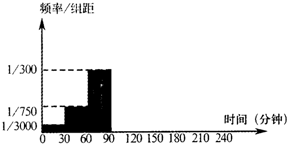
| 利用时间充分 | 利用时间不充分 | 总计 | |
| 走读生 | 50 | ||
| 住宿生 | 10 | ||
| 总计 | 60 | 100 |
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com