
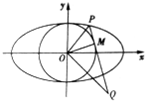
 在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点A($\sqrt{6}$,1),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.
在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点A($\sqrt{6}$,1),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.分析 (Ⅰ)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点A($\sqrt{6}$,1),列出方程组,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)由圆O的方程为x2+y2=4,设点Q的纵坐标为t,则Q(2,t),当MP⊥x轴时,求出t=-2$\sqrt{2}$;当PM不垂直于x轴时,设直线OP:y=kx(k>0,x>0),则直线OQ:y=-$\frac{1}{k}x$,由|OP|•|OQ|=|PQ|•|OM|,能求出点Q的纵坐标的值.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点A($\sqrt{6}$,1),
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{6}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=8,b2=4,
∴椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
(Ⅱ)由(Ⅰ)得圆O的方程为x2+y2=4,
①设点Q的纵坐标为t,则Q(2,t),当MP⊥x轴时,
∵点P在椭圆C上,且在第一象限内,∴P(2,$\sqrt{2}$),
∵$\overrightarrow{OQ}•\overrightarrow{OP}=4+\sqrt{2}t=0$,解得t=-2$\sqrt{2}$.
②当PM不垂直于x轴时,设直线OP:y=kx(k>0,x>0),
∴直线OQ:y=-$\frac{1}{k}x$,
则P(x0,kx0),Q(-tx,t),
在△OPQ中,|OP|•|OQ|=|PQ|•|OM|,
∴$\sqrt{{{x}_{0}}^{2}+{k}^{2}{{x}_{0}}^{2}}•\sqrt{{t}^{2}+{k}^{2}{t}^{2}}$=2$\sqrt{({x}_{0}+tx)^{2}+(k{x}_{0}-t)^{2}}$,
即${{(x}_{0}}^{2}+{k}^{2}{x}_{0}{\;}^{2})({t}^{2}+{k}^{2}{t}^{2})$=4[(x0+kt)2+(kx0-t)2],
${{x}_{0}}^{2}{t}^{2}(1+{k}^{2})^{2}=4({{x}_{0}}^{2}+{k}^{2}{t}^{2}+{k{{\;}^{2}x}_{0}}^{2}+{t}^{2})$,
∴${{x}_{0}}^{2}{t}^{2}(1+{k}^{2})=4({{x}_{0}}^{2}+{t}^{2})$,∴${{x}_{0}}^{2}{t}^{2}+{{x}_{0}}^{2}{k}^{2}{t}^{2}-4{{x}_{0}}^{2}-4{t}^{2}=0$,
又由$\frac{{{x}_{0}}^{2}}{8}+\frac{{k}^{2}{{x}_{0}}^{2}}{4}=1$,∴${{x}_{0}}^{2}{t}^{2}+{{x}_{0}}^{2}{k}^{2}{t}^{2}-4{{x}_{0}}^{2}-4{t}^{2}=0$,
又由$\frac{{{x}_{0}}^{2}}{8}+\frac{{k}^{2}{{x}_{0}}^{2}}{4}=1$,∴${k}^{2}{{x}_{0}}^{2}=4-\frac{{{x}_{0}}^{2}}{2}$,
∴${{x}_{0}}^{2}{t}^{2}+(4-\frac{{{x}_{0}}^{2}}{2}){t}^{2}-4{{x}_{0}}^{2}-4{t}^{2}=0$,∴$\frac{{{x}_{0}}^{2}{t}^{2}}{2}-4{{x}_{0}}^{2}$=0,
∴t2=8,解得t=$±2\sqrt{2}$.
∴点Q的纵坐标的值为$±2\sqrt{2}$.
点评 本题考查椭圆方程的求法,考查点的纵坐标的求法,是中档题,解题时要认真审题,注意椭圆性质、直线方程、椭圆和直线的位置关系的合理运用.


科目:高中数学 来源: 题型:选择题
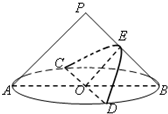 如图,在底面半径和高均为2的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为2的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\frac{{\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,|x0|+x${\;}_{0}^{2}$≥0 | B. | ?x0∈R,|x0|+x${\;}_{0}^{2}$<0 | ||
| C. | ?x∈R,|x|+x2<0 | D. | ?x∈R,|x|+x2≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆 C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左顶点为A1,右焦点为F2,过点 F2作垂直于x轴的直线交椭圆C于M、N两点,直线 A1M的斜率为$\frac{1}{2}$
如图,已知椭圆 C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左顶点为A1,右焦点为F2,过点 F2作垂直于x轴的直线交椭圆C于M、N两点,直线 A1M的斜率为$\frac{1}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
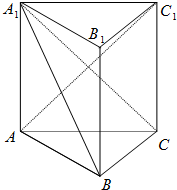 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0°<A≤30° | B. | 0°<A≤45° | ||
| C. | 0°<A≤60° 或120°≤A<180° | D. | 0°<A≤60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com