
| 利用时间充分 | 利用时间不充分 | 总计 | |
| 走读生 | 50 | ||
| 住宿生 | 10 | ||
| 总计 | 60 | 100 |
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
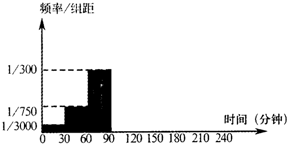
分析 (1)把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准,对抽取的100名学生,完成下列2×2列联表,求出K2,由K2>3.841,得到有95%的把握认为学生利用时间是否充分与走读、住宿有关.
(2)设第i组的频率为Pi(i=1,2,…,8),推导出第①组1人,第②组4人,第③组10人,从而X的所有可能取值为0,1,2,3,$P(X=i)=\frac{{C_5^iC_{10}^{3-i}}}{{C_{15}^3}}(i=0,1,2,3)$,由此能求出X的分布列和数学期望.
解答 解:(1)把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准,对抽取的100名学生,完成下列2×2列联表如下:
| 利用时间充分 | 利用时间不充分 | 总计 | |
| 走读生 | 50 | 25 | 75 |
| 住宿生 | 10 | 15 | 25 |
| 总计 | 60 | 40 | 100 |
| P | 0 | 1 | 2 | 3 |
| X | $\frac{24}{91}$ | $\frac{45}{91}$ | $\frac{20}{91}$ | $\frac{2}{91}$ |
点评 本题考查独立性质检验的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意超几何分布的性质的合理运用.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 增加了$\frac{1}{2(k+1)}$ | B. | 增加了$\frac{1}{2k+1}$+$\frac{1}{2k+2}$ | ||
| C. | 增加了$\frac{1}{2k+1}$+$\frac{1}{2k+2}$,但减少了$\frac{1}{k+1}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,|x0|+x${\;}_{0}^{2}$≥0 | B. | ?x0∈R,|x0|+x${\;}_{0}^{2}$<0 | ||
| C. | ?x∈R,|x|+x2<0 | D. | ?x∈R,|x|+x2≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆 C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左顶点为A1,右焦点为F2,过点 F2作垂直于x轴的直线交椭圆C于M、N两点,直线 A1M的斜率为$\frac{1}{2}$
如图,已知椭圆 C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左顶点为A1,右焦点为F2,过点 F2作垂直于x轴的直线交椭圆C于M、N两点,直线 A1M的斜率为$\frac{1}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
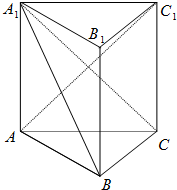 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “x=-1”是“x2-5x-6=0”的根的逆命题为假命题 | |
| C. | 若p∧q为假命题,则p、q均为假命题 | |
| D. | 若命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com