
分析 先后两次出现的点数中有4的事件分三类:第一次出现的点数是4,第二次不是4的有5种情况,第一次出现的点数不是4,第二次是4的也有5种情况,两次出现的点数都是4的只有1种情况,使方程x2+mx+n=0有两个不相等实根要满足△=m2-4n>0,由此能求出使方程x2+mx+n=0有两个不相等实根的概率.
解答 解:先后两次出现的点数中有4的事件分三类:
第一次出现的点数是4,第二次不是4的有5种情况,
第一次出现的点数不是4,第二次是4的也有5种情况,
两次出现的点数都是4的只有1种情况,
所以总数有N=5+5+1=11.
使方程x2+mx+n=0有两个不相等实根要满足△=m2-4n>0,
当m=4时,n=1,2,3,当n=4时,m=5,6,
∴使方程x2+mx+n=0有两个不相等实根包含的基本事件个数M=3+2=5,
∴使方程x2+mx+n=0有两个不相等实根的概率p=$\frac{M}{N}=\frac{5}{11}$.
故答案为:$\frac{5}{11}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意分类讨论思想和等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,|x0|+x${\;}_{0}^{2}$≥0 | B. | ?x0∈R,|x0|+x${\;}_{0}^{2}$<0 | ||
| C. | ?x∈R,|x|+x2<0 | D. | ?x∈R,|x|+x2≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
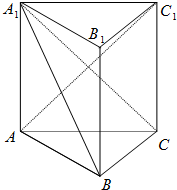 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “x=-1”是“x2-5x-6=0”的根的逆命题为假命题 | |
| C. | 若p∧q为假命题,则p、q均为假命题 | |
| D. | 若命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
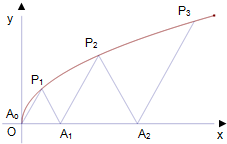 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0°<A≤30° | B. | 0°<A≤45° | ||
| C. | 0°<A≤60° 或120°≤A<180° | D. | 0°<A≤60° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com