
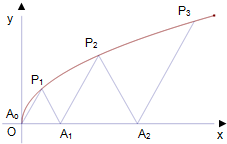
 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).分析 1)由题意可知直线A0P1为y=$\sqrt{3}$x,然后与y2=3x联立可得到P1的坐标,再由△A0A1P1是正三角形可得到A1的坐标得到a1的值,同理可得到a2、a3.
(2)先根据题意可得到关系 ${x_n}=\frac{{{a_{n-1}}+{a_n}}}{2}$,${y_n}=\sqrt{3}•\frac{{{a_n}-{a_{n-1}}}}{2}$,然后根据yn2=3xn得(an-an-1)2=2(an-1+an),从而可猜想数列通项公式an=n(n+1),再由数学归纳法证明即可.
解答 J解:(1)a1=2,a2=6,a3=12;由此猜想:an=n(n+1),
(2)依是意,得${x_n}=\frac{{{a_{n-1}}+{a_n}}}{2}$,${y_n}=\sqrt{3}•\frac{{{a_n}-{a_{n-1}}}}{2}$,
由此及$y_n^2=3{x_n}$得:${(\sqrt{3}•\frac{{{a_n}-{a_{n-1}}}}{2})^2}=\frac{3}{2}({a_n}+{a_{n-1}})$,
即${({a_n}-{a_{n-1}})^2}=2({a_{n-1}}+{a_n})$.
下面用数学归纳法证明猜想:
①当n=1时,猜想显然成立.
②假设当n=k(k∈N*)时,猜想成立,即ak=k(k+1),则当n=k+1时,
∵${({a_{k+1}}-{a_k})^2}=2({a_k}+{a_{k+1}})$,
∴${[{a_{k+1}}-k(k+1)]^2}=2[k(k+1)+{a_{k+1}}]$,
即${a_{k+1}}^2-2({k^2}+k+1){a_{k+1}}+[k(k+1)]•[(k+1)(k+2)=0$,
解得ak+1=(k+1)(k+2)(ak+1=k(k-1)<ak不合题意,舍去)
即当n=k+1时,猜想也成立.
由①②可知,对一切的n∈N*猜想均成立.
点评 本题主要考查求数列通项公式、数列的单调性问题以及二次函数的恒成立问题,考查综合运用能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| A. | ad-bc越小,说明x与y的关系越弱 | B. | ad-bc越大,说明x与y的关系越弱 | ||
| C. | (ad-bc)2越大,说明x与y的关系越强 | D. | (ad-bc)2越小,说明x与y的关系越强 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
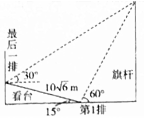 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10$\sqrt{6}$m(如图所示),则旗杆的高度为30m.
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10$\sqrt{6}$m(如图所示),则旗杆的高度为30m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com