
分析 (1)对函数求导,求得函数的单调区间,从而可讨论f(x)的单调性,并求出极值;
(2)先求导函数,研究函数的单调区间,由单调区间求出函数的极大值,结合条件进行判断即可.
解答 解:(1)f′(x)=(2x+a)e-x-e-x(x2+ax+a)=e-x[-x2+(2-a)x]
令f′(x)=0,得x=0或x=2-a>0
列表如下:
| x | (-∞,0) | 0 | (0,2-a) | 2-a | (2-a,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 极小 | 极大 |
点评 本题以函数为载体,考查导数的运用,考查由函数的导数的符号变化研究函数的单调区间与极值,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
 如图,已知椭圆 C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左顶点为A1,右焦点为F2,过点 F2作垂直于x轴的直线交椭圆C于M、N两点,直线 A1M的斜率为$\frac{1}{2}$
如图,已知椭圆 C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左顶点为A1,右焦点为F2,过点 F2作垂直于x轴的直线交椭圆C于M、N两点,直线 A1M的斜率为$\frac{1}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “x=-1”是“x2-5x-6=0”的根的逆命题为假命题 | |
| C. | 若p∧q为假命题,则p、q均为假命题 | |
| D. | 若命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
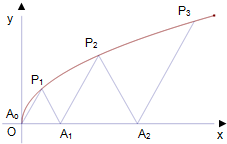 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0°<A≤30° | B. | 0°<A≤45° | ||
| C. | 0°<A≤60° 或120°≤A<180° | D. | 0°<A≤60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∧q是真命题 | B. | 命题p∧¬q是真命题 | ||
| C. | 命题¬p∧q是真命题 | D. | 命题¬p∨¬q是假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com