
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图像在
的图像在![]() 出的切线方程;
出的切线方程;
(2)判断函数![]() 的单调性;
的单调性;
(3)证明:![]() .
.
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(I)当a=2时,先求出![]() 的值,即切线的斜率,然后写出点斜式方程,再化成一般式即可.
的值,即切线的斜率,然后写出点斜式方程,再化成一般式即可.
(II)先求导,可得![]() ,然后再对
,然后再对![]() 和a<0两种情况进行讨论研究其单调性.
和a<0两种情况进行讨论研究其单调性.
(III) 由(Ⅱ)可知,当![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
∴ 当![]() 时,
时,![]() ,即
,即![]()
然后解本题的关键是令![]() (
(![]() ),则
),则 ,
,
又因为![]() ,即
,即![]() ,从而问题得证
,从而问题得证
(Ⅰ)当![]() 时,
时,![]() ,
,
∴![]() ,1分∴
,1分∴![]() ,所以所求的切线的斜率为3. 2分
,所以所求的切线的斜率为3. 2分
又∵![]() ,所以切点为
,所以切点为![]() .3分故所求的切线方程为:
.3分故所求的切线方程为:![]() .4分
.4分
(Ⅱ)∵![]()
![]() ,∴
,∴![]() .①当
.①当![]() 时,∵
时,∵![]() ,∴
,∴![]() ;②当
;②当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ;综上,当
;综上,当![]() 时,函数
时,函数![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增.···· 8分
上单调递增.···· 8分
(Ⅲ)方法一:由(Ⅱ)可知,当![]() 时,
时,![]() 在
在![]() 上单调递增.∴ 当
上单调递增.∴ 当![]() 时,
时,![]() ,即
,即![]() .···························· 10分
.···························· 10分
令![]() (
(![]() ),则
),则 .··············· 11分
.··············· 11分
另一方面,∵![]() ,即
,即![]() ,∴
,∴![]() .∴
.∴![]() (
(![]() ).
).
方法二:构造函数![]() ,
,![]() ············· 9分
············· 9分
∴![]() ,··················· 10分
,··················· 10分
∴当![]() 时,
时,![]() ;∴函数
;∴函数![]() 在
在![]() 单调递增.∴函数
单调递增.∴函数![]() ,即
,即![]() ∴
∴![]() ,
,![]() ,即
,即![]() 2分
2分
令![]() (
(![]() ),则有
),则有![]()


科目:高中数学 来源: 题型:
【题目】如图,一个湖的边界是圆心为![]() 的圆,湖的一侧有一条直线型公路
的圆,湖的一侧有一条直线型公路![]() ,湖上有桥
,湖上有桥![]() (
(![]() 是圆
是圆![]() 的直径).规划在公路
的直径).规划在公路![]() 上选两个点
上选两个点![]() ,并修建两段直线型道路
,并修建两段直线型道路![]() .规划要求:线段
.规划要求:线段![]() 上的所有点到点
上的所有点到点![]() 的距离均不小于圆
的距离均不小于圆![]() 的半径.已知点
的半径.已知点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 和
和![]() (
(![]() 为垂足),测得
为垂足),测得![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).
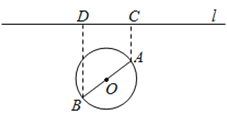
(1)若道路![]() 与桥
与桥![]() 垂直,求道路
垂直,求道路![]() 的长;
的长;
(2)在规划要求下,![]() 和
和![]() 中能否有一个点选在
中能否有一个点选在![]() 处?并说明理由.
处?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P—ABCD中,PA⊥平面ABCD,∠DAB=∠ADC=90°,DC=![]() AB,F,M分别是线段PC,PB的中点.
AB,F,M分别是线段PC,PB的中点.

(1)在线段AB上找出一点N,使得平面CMN∥平面PAD,并给出证明过程;
(2)若PA=![]() AB,DC=
AB,DC=![]() AD,求二面角C—AF—D的余弦值.
AD,求二面角C—AF—D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山东省于2015年设立了水下考古研究中心,以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站,分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。为对刘公岛周边海域水底情况进行详细了解,然后再选择合适的时机下水探摸、打捞,省水下考古中心在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业,其用氧量包含以下三个方面:
米到水底进行考古作业,其用氧量包含以下三个方面:
①下潜平均速度为![]() 米/分钟,每分钟的用氧量为
米/分钟,每分钟的用氧量为![]() 升;
升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.4升;
③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为0.32升.
米/分钟,每分钟用氧量为0.32升.
潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(Ⅰ)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)若![]() ,水底作业时间为20分钟,求总用氧量
,水底作业时间为20分钟,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3-3ax,g(x)=bx2+clnx,且g(x)在点(1,g(1))处的切线方程为2y-1=0.
(1)求g(x)的解析式;
(2)设函数G(x)=![]() 若方程G(x)=a2有且仅有四个解,求实数a的取值范围.
若方程G(x)=a2有且仅有四个解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(1,0)和点B(﹣1,0),![]() ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点.

(1)若x=![]() ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求![]() 的最小值;
的最小值;
(2)若![]() R,求
R,求![]() 的最大值及对应的x值.
的最大值及对应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,将四边形
的中点,将四边形![]() 沿直线
沿直线![]() 进行翻折,给出下列四个结论:①
进行翻折,给出下列四个结论:①![]() ;②
;②![]() ③平面
③平面![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() ,则上述结论可能正确的是( ).
,则上述结论可能正确的是( ).
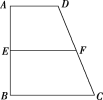
A.①③B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )
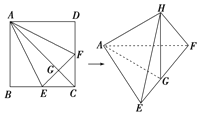
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com