
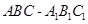 中,
中,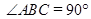 ,
,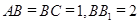 ,求:
,求: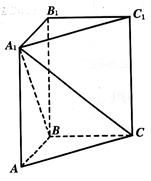
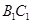 与
与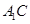 所成角的大小;
所成角的大小; 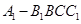 的体积.
的体积.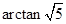 ;(2)
;(2)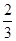 .
.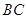 ∥
∥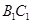 ,
,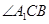 就是我们要求的角(或其补角);(2)一种方法就是直接利用体积公式,四棱锥
就是我们要求的角(或其补角);(2)一种方法就是直接利用体积公式,四棱锥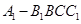 的底面是矩形
的底面是矩形 ,下面要确定高,即找到底面
,下面要确定高,即找到底面 的垂线,由于是直棱柱,因此侧棱
的垂线,由于是直棱柱,因此侧棱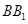 与底面垂直,从而
与底面垂直,从而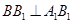 ,题中又有
,题中又有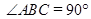 ,即
,即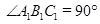 ,从而
,从而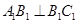 ,故
,故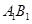 就是底面的垂线,也即高.
就是底面的垂线,也即高.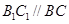 ,所以
,所以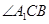 (或其补角)是异面直线
(或其补角)是异面直线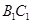 与
与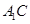 所成角. 1分
所成角. 1分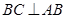 ,
,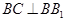 ,所以
,所以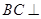 平面
平面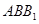 ,所以
,所以 . 3分
. 3分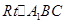 中,
中,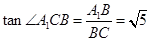 ,所以
,所以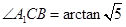 5分
5分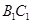 与
与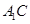 所成角的大小为
所成角的大小为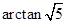 . 6分
. 6分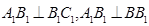
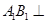 平面
平面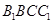 9分
9分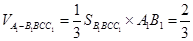 12分
12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com