
分析 (Ⅰ)求出函数h(x)的导数,问题转化为函数m(x)=2x2-2ax+a)≥0在区间($\frac{1}{2}$,1)上恒成立,(x>0),结合二次函数的性质求出a的范围即可;
(Ⅱ)F(x)max=F(1)=2-2a,存在x0∈(0,1]使得不等式F(x0)>m(a-a2)-lna成立,即2-2a>m(a-a2)-lna,分离参数m,得到m>$\frac{2-2a+lna}{a{-a}^{2}}$恒成立,构造函数g(a)=$\frac{2-2a+lna}{a{-a}^{2}}$,利用导数求解即可转化为最值即可判断.
解答 解:(Ⅰ)h(x)=alnx+x2-2ax+1,(x>0),
h′(x)=$\frac{a}{x}$+2x-2a=$\frac{{2x}^{2}-2ax+a}{x}$,
令m(x)=2x2-2ax+a,(x>0),
若h(x)在区间($\frac{1}{2}$,1)上是增函数,
只需m(x)≥0在区间($\frac{1}{2}$,1)上恒成立,
函数m(x)的对称轴x=$\frac{a}{2}$,
当$\frac{a}{2}$<$\frac{1}{2}$即a<1时,
只需m($\frac{1}{2}$)≥0,而m($\frac{1}{2}$)=$\frac{1}{2}$>0,
故a<1满足条件,
当$\frac{a}{2}$>1即a>2时,
只需m(1)=2-a≥0,解得a≤2,不合题意,
当$\frac{1}{2}$≤$\frac{a}{2}$≤1即1≤a≤2时,
只需△=4a2-8a≤0,解得:0≤a≤2,
综上,a≤2;
(Ⅱ)F(x)=lnx+x2-2ax+1,(x>0),
∵a∈(1,$\sqrt{2}$),$\frac{1}{x}$+2x-2a>0,
∴f′(x)>0,f(x)在(0,1]单调递增,
f(x)max=f(1)=2-2a,
存在x0∈(0,1]使得不等式F(x0)>m(a-a2)-lna成立,
即2-2a>m(a-a2)-lna,
∵任意的a∈(1,$\sqrt{2}$),∴a-a2<0,
即m>$\frac{2}{a}$+$\frac{lna}{a{-a}^{2}}$恒成立,
令g(a)=$\frac{2}{a}$+$\frac{lna}{a{-a}^{2}}$,
∵m>$\frac{2-2a+lna}{a{-a}^{2}}$恒成立
最后化简为g′(a)=$\frac{(2a-1)lna-({2a}^{2}-3a+1)}{{(a{-a}^{2})}^{2}}$=$\frac{(2a-1)(lna-a+1)}{{(a{-a}^{2})}^{2}}$,
∵任意的a∈(1,$\sqrt{2}$),$\frac{(2a-1)(lna-a+1)}{{(a{-a}^{2})}^{2}}$>0,
∴g(a)=$\frac{2}{a}$+$\frac{lna}{a{-a}^{2}}$,a∈(1,$\sqrt{2}$)是增函数.
∴g(x)<g($\sqrt{2}$)=$\frac{2}{\sqrt{2}}$+$\frac{ln\sqrt{2}}{\sqrt{2}-2}$=$\sqrt{2}$-$\frac{(2+\sqrt{2})ln2}{4}$,
∴实数m的取值范围是($\sqrt{2}$-$\frac{(2+\sqrt{2})ln2}{4}$,+∞).
点评 用导数工具讨论函数的单调性,是求函数的值域和最值的常用方法,同学们在做题的同时,可以根据单调性,结合函数的草图来加深对题意的理解.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 134 | 112 | 117 | 126 | 128 | 124 | 122 | 116 | 113 | 107 |
| 116 | 132 | 127 | 128 | 126 | 121 | 120 | 118 | 108 | 110 |
| 133 | 130 | 124 | 116 | 117 | 123 | 122 | 120 | 112 | 112 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
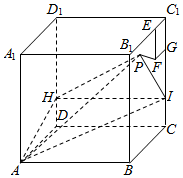 如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )
如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )| A. | $\frac{2\sqrt{17}}{3}$ | B. | $\frac{25}{6}$ | C. | $\frac{2\sqrt{17}}{3}$(10-3$\sqrt{2}$) | D. | $\frac{20}{3}$-2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com