
某中学有A、B、C、D、E五名同学在高三“一检”中的名次依次为1,2,3,4,5名,“二检”中的前5名依然是这五名同学.
(1)求恰好有两名同学排名不变的概率;
(2)如果设同学排名不变的同学人数为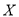 ,求
,求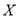 的分布列和数学期望.
的分布列和数学期望.
(1)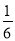 ;(2)
;(2)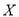 分布列为
分布列为
| 0 | 1 | 2 | 3 | 5 |
|
|
|
|
|
|
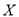 的数学期望
的数学期望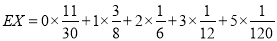
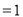 .
.
【解析】
试题分析:(1)第二次排名的基本事件总数为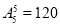 ,恰有2名同学排名不变所包含的基本事件数有:
,恰有2名同学排名不变所包含的基本事件数有: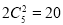 种(先确定哪两个同学的排名不变,排名变化的三名同学只有两种情况),从而根据古典概型的概率计算公式即可求得所求的概率;(2)先确定
种(先确定哪两个同学的排名不变,排名变化的三名同学只有两种情况),从而根据古典概型的概率计算公式即可求得所求的概率;(2)先确定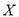 所有可能的取值
所有可能的取值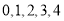 ,再分别求解
,再分别求解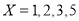 时的概率,方法与(1)同,仍属古典概率问题,最后再根据概率和为1计算出
时的概率,方法与(1)同,仍属古典概率问题,最后再根据概率和为1计算出 ,进而列出分布列,根据期望的计算公式计算出期望即可.
,进而列出分布列,根据期望的计算公式计算出期望即可.
(1)第二次排名,恰好有两名同学排名不变的情况数为: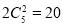 (种)
(种)
第二次排名情况总数为: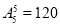 ,所以恰好有两名同学排名不变的概率为
,所以恰好有两名同学排名不变的概率为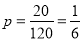
(2)第二次同学排名不变的同学人数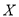 可能的取值为:5,3,2,1,0
可能的取值为:5,3,2,1,0
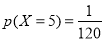
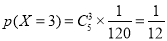
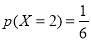
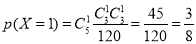
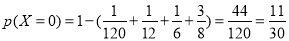
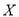 分布列为
分布列为
| 0 | 1 | 2 | 3 | 5 |
|
|
|
|
|
|
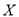 的数学期望
的数学期望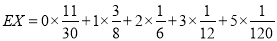
 12分.
12分.
考点:1.古典概型;2.分布列;3.分布期望.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届河北唐山一中高二下学期期末考试理科数学试卷(解析版) 题型:选择题
.设随机变量ξ服从正态分布 ,若
,若 =
= ,则c的值是( )
,则c的值是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末理数学卷(解析版) 题型:选择题
条件 ,条件
,条件 ,则p是q的( ).
,则p是q的( ).
A.充分不必要条件B.必要不充分条件  充要条件 D.既不充分又不必要条件
充要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末文数学卷(解析版) 题型:选择题
已知 在区间(0,+∞)上是减函数,那么
在区间(0,+∞)上是减函数,那么 与
与 的大小关系是( ).
的大小关系是( ).
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
甲袋中有8个白球,4个红球;乙袋中有6个白球,6个红球,从每袋中任取1个球,取得同色球的概率是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com