
(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如下图所示.


(1)上表是年龄的频数分布表,求正整数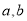 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
(1)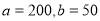 ,(2) 1人,1人,4人,(3)
,(2) 1人,1人,4人,(3)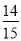 .
.
【解析】
试题分析:(1)在频率分布直方图,小长方形的面积是表示数据落在小组内的频率,它的高是频率与组距的比;(2)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;
试题解析:(1)由题设可知, ,
,
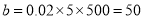 . 2分
. 2分
(2) 因为第1,2,3组共有50+50+200=300人,
利用分层抽样在300名学生中抽取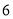 名学生,每组抽取的人数分别为:
名学生,每组抽取的人数分别为:
第1组的人数为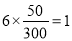 ,第2组的人数为
,第2组的人数为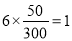 ,
,
第3组的人数为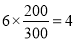 ,
,
所以第1,2,3组分别抽取1人,1人,4人. 6分
(3)设第1组的1位同学为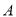 ,第2组的1位同学为
,第2组的1位同学为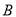 ,第3组的4位同学为
,第3组的4位同学为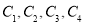 ,则从六位同学中抽两位同学有:
,则从六位同学中抽两位同学有:
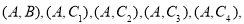
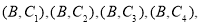
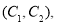
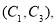
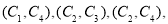
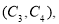 共
共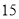 种可能. 9分
种可能. 9分
其中2人年龄都不在第3组的有: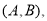 共1种可能,
共1种可能,
所以至少有1人年龄在第3组的概率为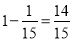 . 12分 .
. 12分 .
考点:频率分布直方图与古典概型问题.


科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知 是R上的偶函数,若将
是R上的偶函数,若将 的图象向右平移一个单位,则得到一个奇函数的图像,若
的图象向右平移一个单位,则得到一个奇函数的图像,若 则
则 =
=
(A)0 (B)1 (C)-1 (D)-1004.5
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试文科数学试卷(解析版) 题型:填空题
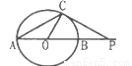
如图,⊙O的直径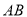 =6cm,
=6cm,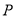 是延长线上的一点,过点
是延长线上的一点,过点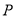 作⊙O的切线,切点为
作⊙O的切线,切点为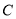 ,连结
,连结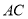 ,若
,若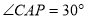 ,则
,则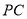 = .
= .
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设{ }为公比
}为公比 的等比数列,若
的等比数列,若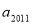 和
和 是方程
是方程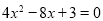 的两根,则
的两根,则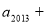
 ( )
( )
A.25 B.18 C.10 D.9
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期期中考试数学试卷(解析版) 题型:解答题
如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,求它落在扇形外正方形内的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com