
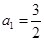 ,公差
,公差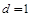 ,求满足
,求满足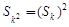 的正整数k;
的正整数k;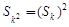 成立
成立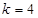 (Ⅱ)见解析
(Ⅱ)见解析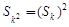 成立”这句话将k取两个特殊值确定出等差数列的首项和公差,但没有认识到求解出的等差数列仅是对已知条件成立的必要条件,但不是条件成立的充分条件。还应进一步的由特殊到一般。
成立”这句话将k取两个特殊值确定出等差数列的首项和公差,但没有认识到求解出的等差数列仅是对已知条件成立的必要条件,但不是条件成立的充分条件。还应进一步的由特殊到一般。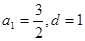 时
时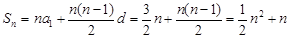
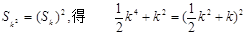 ,即
,即 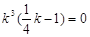 又
又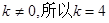 .
.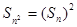 中分别取k=1,2,得
中分别取k=1,2,得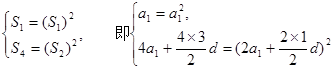
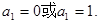 当
当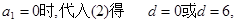
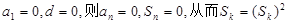 成立 ,
成立 ,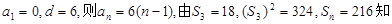
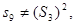 故所
故所
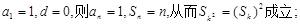
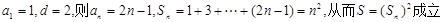 .
.

科目:高中数学 来源:不详 题型:解答题
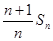
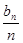 的最小值.
的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com