
分析 (1)由$\overrightarrow{a}$⊥$\overrightarrow{b}$可得$\overrightarrow{a}•\overrightarrow{b}$=-2+2x=0解方程可得x的;
(2)当向量$\overrightarrow{a}$与(4$\overrightarrow{a}$+$\overrightarrow{b}$)的夹角是锐角时,$\overrightarrow{a}$•(4$\overrightarrow{a}$+$\overrightarrow{b}$)>0,解关于x的不等式排除同向可得x的范围,由模长公式和二次函数的最值可得.
解答 解:(1)∵$\overrightarrow a$=(1,2),$\overrightarrow b$=(-2,x),
当$\overrightarrow{a}$⊥$\overrightarrow{b}$时,$\overrightarrow{a}•\overrightarrow{b}$=-2+2x=0,
解方程可得x的值为1;
(2)4$\overrightarrow{a}$+$\overrightarrow{b}$=(2,8+x),
当向量$\overrightarrow{a}$与(4$\overrightarrow{a}$+$\overrightarrow{b}$)的夹角是锐角时,$\overrightarrow{a}$•(4$\overrightarrow{a}$+$\overrightarrow{b}$)>0,
∴2+16+2x>0,解得x>-9,
当$\overrightarrow{a}$与(4$\overrightarrow{a}$+$\overrightarrow{b}$)共线时,1×(8+x)=2×2,解得x=-4,
此时4$\overrightarrow{a}$+$\overrightarrow{b}$=(2,4),与向量$\overrightarrow a$=(1,2)同向,
满足$\overrightarrow{a}$•(4$\overrightarrow{a}$+$\overrightarrow{b}$)>0但向量夹角不是锐角,应舍去,
∴x的取值范围为x>-9且x≠-4,
∴|$\overrightarrow{b}$|=$\sqrt{(-2)^{2}+{x}^{2}}$∈[2,+∞)
点评 本题考查平面向量的夹角,涉及向量垂直和模长公式以及二次函数的最值,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(文)试卷(解析版) 题型:解答题
选修4—4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(1)把 的参数方程化为极坐标方程 ;
的参数方程化为极坐标方程 ;
(2)求 与
与 交点的极坐标(
交点的极坐标(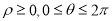 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com