
【题目】如图所示,在△ABC中,B= ![]() ,AC=2
,AC=2 ![]() ,cosC=
,cosC= ![]() .
. 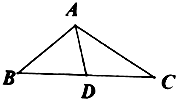
(1)求sin∠BAC的值及BC的长度;
(2)设BC的中点为D,求中线AD的长.
【答案】
(1)解:∵在△ABC中,B= ![]() ,AC=2
,AC=2 ![]() ,cosC=
,cosC= ![]() ,
,
∴sinC= ![]() =
= ![]() ,
,
∴sin∠BAC=sin(B+C)=sinBcosC+cosBsinC= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ;
;
由正弦定理得: ![]() =
= ![]() ,即BC=
,即BC= ![]() =
= 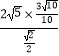 =6
=6
(2)解:在△ADC中,CD= ![]() BC=3,AC=2
BC=3,AC=2 ![]() ,cosC=
,cosC= ![]() ,
,
由余弦定理得:AD2=AC2+DC2﹣2ACDCcosC=20+9﹣2×2 ![]() ×3×
×3× ![]() =5,
=5,
则AD= ![]()
【解析】(1)由cosC的值求出sinC的值,根据诱导公式得到sin∠BAC=sin(B+C),利用两角和与差的正弦函数公式化简,将各自的值代入计算求出值,再由sin∠BAC,sinB,以及AC的长,利用正弦定理求出BC的长即可;(2)根据D为BC中点,求出CD的长,再由AC与cosC的值,利用余弦定理求出AD的长即可.
【考点精析】认真审题,首先需要了解余弦定理的定义(余弦定理:![]() ;
;![]() ;
;![]() ).
).


科目:高中数学 来源: 题型:
【题目】为研究患肺癌与是否吸烟有关,做了一次相关调查,其中部分数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
(1)若吸烟不患肺癌的有![]() 人,现从患肺癌的人中用分层抽样的方法抽取
人,现从患肺癌的人中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行调查,求这两人都是吸烟患肺癌的概率;
人进行调查,求这两人都是吸烟患肺癌的概率;
(2)若研究得到在犯错误概率不超过![]() 的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
附: 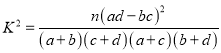 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在静水中游泳,速度为4![]() 公里/小时,他在水流速度为4公里/小时的河中游泳.
公里/小时,他在水流速度为4公里/小时的河中游泳.
(1)若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有丨FA丨=丨FD丨.当点A的横坐标为3时,△ADF为正三角形.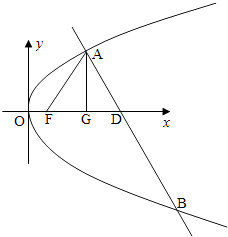
(1)求C的方程;
(2)若直线l1∥l,且l1和C有且只有一个公共点E,
(ⅰ)证明直线AE过定点,并求出定点坐标;
(ⅱ)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个圆柱形乒乓球筒,高为![]() 厘米,底面半径为
厘米,底面半径为![]() 厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com