练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在锐角△ABC中，内角A，B，C所对的边分别为a，b，c，已知 a=2csinA．
    （1）求角C的值；
    （2）若c= ，且S△ABC= ，求a+b的值．

    【答案】
    （1）解：由 a=2csinA及正弦定理，得 sinA=2sinCsinA，

    ∵sinA≠0，

    ∴sinC= ．

    又∵△ABC是锐角三角形，

    ∴C= ．


    （2）解：∵c= ，C= ，

    ∴由面积公式，得 absin = ，即ab=6．①

    由余弦定理，得a2+b2﹣2abcos =7，

    即a2+b2﹣ab=7．②

    由②变形得（a+b）2=3ab+7．③

    将①代入③得（a+b）2=25，故a+b=5


    【解析】（1）由 a=2csinA及正弦定理得 sinA=2sinCsinA，又sinA≠0，可sinC= ．又△ABC是锐角三角形，即可求C．（2）由面积公式，可解得ab=6，由余弦定理，可解得a2+b2﹣ab=7，联立方程即可解得a+b的值的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知曲线： ， ： （），从上的点作轴的垂线，交于点，再从点作轴的垂线，交于点.设， ， .

    （Ⅰ）求数列的通项公式；

    （Ⅱ）记，数列的前项和为，求证： ；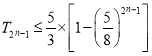

    （Ⅲ）若已知（），记数列的前项和为，数列的前项和为，试比较与的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在△ABC中，B= ，AC=2 ，cosC= ．

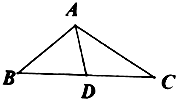
    （1）求sin∠BAC的值及BC的长度；
    （2）设BC的中点为D，求中线AD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）求曲线在点处的切线方程；

    （Ⅱ）是否存在正整数，使得在上恒成立？若存在，求出的最大值并给出推导过程，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}满足a2=0，a6+a8=﹣10．
    （1）求数列{an}的通项公式；
    （2）求数列{ }的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解答
    （1）解不等式 ＜0．
    （2）若关于不等式x2﹣4ax+4a2+a≤0的解集为，则实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用0、1、2、3、4这五个数字，可以组成多少个满足下列条件的没有重复数字的五位数？
    （1）奇数；
    （2）比21034大的偶数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中正确的是（ ）
    A. 的最小值是2
    B. 的最小值是2
    C. 的最小值是
    D. 的最大值是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在锐角△ABC中，a，b，c分别为角A，B，C的对边，且4sin2 ﹣cos2A= ．
    （1）求角A的大小；
    （2）若BC边上高为1，求△ABC面积的最小值？

    查看答案和解析>>

    同步练习册答案