
ЁОЬтФПЁПвбжЊХзЮяЯпCЃКy2=2pxЃЈpЃО0ЃЉЕФНЙЕуЮЊFЃЌAЮЊCЩЯвьгкдЕуЕФШЮвтвЛЕуЃЌЙ§ЕуAЕФжБЯпlНЛCгкСэвЛЕуBЃЌНЛxжсЕФе§АыжсгкЕуDЃЌЧвгаиFAи=иFDиЃЎЕБЕуAЕФКсзјБъЮЊ3ЪБЃЌЁїADFЮЊе§Ш§НЧаЮЃЎ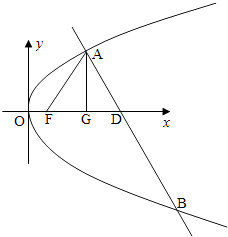
ЃЈ1ЃЉЧѓCЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпl1ЁЮlЃЌЧвl1КЭCгаЧвжЛгавЛИіЙЋЙВЕуEЃЌ
ЃЈЂЁЃЉжЄУїжБЯпAEЙ§ЖЈЕуЃЌВЂЧѓГіЖЈЕузјБъЃЛ
ЃЈЂЂЃЉЁїABEЕФУцЛ§ЪЧЗёДцдкзюаЁжЕЃПШєДцдкЃЌЧыЧѓГізюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКЕБЕуAЕФКсзјБъЮЊ3ЪБЃЌЙ§ЕуAзїAGЁЭxжсгкGЃЌ
AЃЈ3ЃЌ ![]() ЃЉЃЌFЃЈ
ЃЉЃЌFЃЈ ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЎ
ЃЎ
ЁпЁїADFЮЊе§Ш§НЧаЮЃЌ
Ёр ![]() ЃЎ
ЃЎ
гжЁп ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёрp=2ЃЎ
ЁрCЕФЗНГЬЮЊy2=4xЃЎ
ЕБDдкНЙЕуFЕФзѓВрЪБЃЌ ![]() ЃЎ
ЃЎ
гж|FD|=2|FG|=2ЃЈ ![]() Љ3ЃЉ=pЉ6ЃЌ
Љ3ЃЉ=pЉ6ЃЌ
ЁпЁїADFЮЊе§Ш§НЧаЮЃЌ
Ёр3+ ![]() =pЉ6ЃЌНтЕУp=18ЃЌ
=pЉ6ЃЌНтЕУp=18ЃЌ
ЁрCЕФЗНГЬЮЊy2=36xЃЎДЫЪБЕуDдкxжсИКАыжсЃЌВЛГЩСЂЃЌЩсЃЎ
ЁрCЕФЗНГЬЮЊy2=4xЃЎ
ЃЈ2ЃЉ
НтЃКЃЈЂЁЃЉЩшAЃЈx1ЃЌy1ЃЉЃЌ|FD|=|AF|=x1+1ЃЌ
ЁрDЃЈx1+2ЃЌ0ЃЉЃЌ
ЁрkAD=Љ ![]() ЃЎ
ЃЎ
гЩжБЯпl1ЁЮlПЩЩшжБЯпl1ЗНГЬЮЊ ![]() ЃЌ
ЃЌ
СЊСЂЗНГЬ  ЃЌЯћШЅxЕУ
ЃЌЯћШЅxЕУ ![]() Ђй
Ђй
гЩl1КЭCгаЧвжЛгавЛИіЙЋЙВЕуЕУЁї=64+32y1m=0ЃЌЁрy1m=Љ2ЃЌ
етЪБЗНГЬЂйЕФНтЮЊ ![]() ЃЌДњШы
ЃЌДњШы ![]() ЕУx=m2ЃЌЁрEЃЈm2ЃЌ2mЃЉЃЎ
ЕУx=m2ЃЌЁрEЃЈm2ЃЌ2mЃЉЃЎ
ЕуAЕФзјБъПЩЛЏЮЊ ![]() ЃЌжБЯпAEЗНГЬЮЊyЉ2m=
ЃЌжБЯпAEЗНГЬЮЊyЉ2m= ![]() ЃЈxЉm2ЃЉЃЌ
ЃЈxЉm2ЃЉЃЌ
МД ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
ЁржБЯпAEЙ§ЖЈЕуЃЈ1ЃЌ0ЃЉЃЛ
ЃЈЂЂЃЉжБЯпABЕФЗНГЬЮЊ ![]() ЃЌМД
ЃЌМД ![]() ЃЎ
ЃЎ
СЊСЂЗНГЬ  ЃЌЯћШЅxЕУ
ЃЌЯћШЅxЕУ ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
гЩЃЈЂЁЃЉЕуEЕФзјБъЮЊ ![]() ЃЌЕуEЕНжБЯпABЕФОрРыЮЊЃК
ЃЌЕуEЕНжБЯпABЕФОрРыЮЊЃК
 =
=  ЃЌ
ЃЌ
ЁрЁїABEЕФУцЛ§ ![]() =
= ![]() ЃЌ
ЃЌ
ЕБЧвНіЕБy1=ЁР2ЪБЕШКХГЩСЂЃЌ
ЁрЁїABEЕФУцЛ§зюаЁжЕЮЊ16ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉИљОнХзЮяЯпЕФНЙАыОЖЙЋЪНЃЌНсКЯЕШБпШ§НЧаЮЕФаджЪЃЌЧѓГіЕФpжЕЃЛЃЈ2ЃЉЃЈЂЁЃЉЩшГіЕуAЕФзјБъЃЌЧѓГіжБЯпABЕФЗНГЬЃЌРћгУжБЯпl1ЁЮlЃЌЧвl1КЭCгаЧвжЛгавЛИіЙЋЙВЕуEЃЌЧѓГіЕуEЕФзјБъЃЌаДГіжБЯпAEЕФЗНГЬЃЌНЋЗНГЬЛЏЮЊЕуаБЪНЃЌПЩЧѓГіЖЈЕуЃЛЃЈЂЂЃЉ РћгУЯвГЄЙЋЪНЧѓГіЯвABЕФГЄЖШЃЌдйЧѓЕуEЕНжБЯпABЕФОрРыЃЌЕУЕНЙигкУцЛ§ЕФКЏЪ§ЙиЯЕЪНЃЌдйРћгУЛљБОВЛЕШЪНЧѓзюаЁжЕЃЎ


 ФмПМЪдЦкФЉГхДЬОэЯЕСаД№АИ
ФмПМЪдЦкФЉГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЬжТлКЏЪ§![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() ЕФзюжЕЃЎ
ЕФзюжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЉABCDжаЃЌPAЁЭЕзУцABCDЃЌABЁЭADЃЌACЁЭCDЃЌЁЯABC=60ЁуЃЌPA=AB=BCЃЌEЪЧPCЕФжаЕуЃЎ
ЃЈЂёЃЉжЄУїЃКCDЁЭAEЃЛ
ЃЈЂђЃЉжЄУїЃКPDЁЭЦНУцABEЃЛ
ЃЈЂѓЃЉЧѓЖўУцНЧAЉPDЉCЕФе§ЧажЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШ§РтжљABCЉA1B1C1жаЃЌCA=CBЃЌAB=AA1 ЃЌ ЁЯBAA1=60ЁуЃЎ
ЃЈЂёЃЉжЄУїЃКABЁЭA1CЃЛ
ЃЈЂђЃЉШєЦНУцABCЁЭЦНУцAA1B1BЃЌAB=CBЃЌЧѓжБЯпA1CгыЦНУцBB1C1CЫљГЩНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁїABCжаЃЌB= ![]() ЃЌAC=2
ЃЌAC=2 ![]() ЃЌcosC=
ЃЌcosC= ![]() ЃЎ
ЃЎ 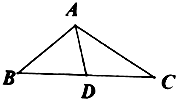
ЃЈ1ЃЉЧѓsinЁЯBACЕФжЕМАBCЕФГЄЖШЃЛ
ЃЈ2ЃЉЩшBCЕФжаЕуЮЊDЃЌЧѓжаЯпADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§Са{an}жаЃЌanЃО0ЃЌa1= ![]() ЃЌШчЙћan+1ЪЧ1гы
ЃЌШчЙћan+1ЪЧ1гы ![]() ЕФЕШБШжаЯюЃЌФЧУДa1+
ЕФЕШБШжаЯюЃЌФЧУДa1+ ![]() +
+ ![]() +
+ ![]() +Ё
+Ё ![]() ЕФжЕЪЧ ЃЎ
ЕФжЕЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉЧѓЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈЂђЃЉЪЧЗёДцдке§ећЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() дк
дк![]() ЩЯКуГЩСЂЃПШєДцдкЃЌЧѓГі
ЩЯКуГЩСЂЃПШєДцдкЃЌЧѓГі![]() ЕФзюДѓжЕВЂИјГіЭЦЕМЙ§ГЬЃЌШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФзюДѓжЕВЂИјГіЭЦЕМЙ§ГЬЃЌШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтД№
ЃЈ1ЃЉНтВЛЕШЪН ![]() ЃМ0ЃЎ
ЃМ0ЃЎ
ЃЈ2ЃЉШєЙигкВЛЕШЪНx2Љ4ax+4a2+aЁм0ЕФНтМЏЮЊЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌADЁЮBCЃЌAD=ABЃЌЁЯBCD=45ЁуЃЌЁЯBAD=90ЁуЃЌНЋЁїABDбиBDелЦ№ЃЌЪЙЦНУцABDЁЭЦНУцBCDЃЌЙЙГЩЫФУцЬхAЉBCDЃЌдђдкЫФУцЬхABCDжаЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ 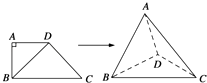
A.ЦНУцABDЁЭЦНУцABC
B.ЦНУцADCЁЭЦНУцBDC
C.ЦНУцABCЁЭЦНУцBDC
D.ЦНУцADCЁЭЦНУцABC
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com