练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数．

    （1）讨论函数的单调性；

    （2）若，求函数的最值．

    【答案】（1）详见解析；（2）详见解析.

    【解析】试题分析：（1）先求导，分类讨论即可求出函数的单调区间；（2）求导，根据导数和函数的最值得关系即可求出，注意分类讨论．

    试题解析：（1），令，得，

    ①若，则恒成立，所以函数在上单调递增；

    ②若，则由，得；由，得，

    所以函数在上单调递增，在上单调递减；

    ③若，则由，得；由，得，

    所以函数在上单调递增，在上单调递减；

    ④若，则恒成立，所以函数在上单调递减.

    （2）若，

    ①当时， ，由（1）得，函数在上单调递增，在上单调递减，

    故时，函数有最大值，无最小值；

    ②当时， ，由（1）得，函数在上单调递增，在上单调递减，

    故时，函数有最小值，无最大值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出下列五个命题：
    ①x= 是函数y=2sin（2x﹣ ）的一条对称轴；
    ②函数y=tanx的图象关于点（ ，0）对称；
    ③正弦函数在第一象限为增函数
    ④函数y=cos（x﹣ ）的一个单调增区间是（﹣ ， ）
    以上四个命题中正确的有（填写正确命题前面的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l：x﹣my+3=0和圆C：x2+y2﹣6x+5=0
    （1）当直线l与圆C相切时，求实数m的值；
    （2）当直线l与圆C相交，且所得弦长为 时，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校有体育特长生25人，美术特长生35人，音乐特长生40人．用分层抽样的方法从中抽取40人，则抽取的体育特长生、美术特长生、音乐特长生的人数分别为（　　）
    A.8，14，18
    B.9，13，18
    C.10，14，16
    D.9，14，17

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为研究患肺癌与是否吸烟有关，做了一次相关调查，其中部分数据丢失，但可以确定的是不吸烟人数与吸烟人数相同，吸烟患肺癌人数占吸烟总人数的；不吸烟的人数中，患肺癌与不患肺癌的比为．

    （1）若吸烟不患肺癌的有人，现从患肺癌的人中用分层抽样的方法抽取人，再从这人中随机抽取人进行调查，求这两人都是吸烟患肺癌的概率；

    （2）若研究得到在犯错误概率不超过的前提下，认为患肺癌与吸烟有关，则吸烟的人数至少有多少？

    附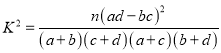： ，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＜0，关于x的一元二次不等式ax2﹣（2+a）x+2＞0的解集为（ ）
    A.{x|x＜ 或x＞1}
    B.{x| ＜x＜1}
    C.{x|x＜1或x＞ }
    D.{x|1＜x＜ }

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】证明下列不等式：
    （1）设a，b，c∈R* ， 且满足条件a+b+c=1，证明： ≥9
    （2）已知a≥0，证明： ＜ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数（）

    （Ⅰ）当时，求在处的切线方程；

    （Ⅱ）求单调区间；

    （Ⅲ）若图象与轴关于， 两点，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2=2px（p＞0）的焦点为F，A为C上异于原点的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D，且有丨FA丨=丨FD丨．当点A的横坐标为3时，△ADF为正三角形．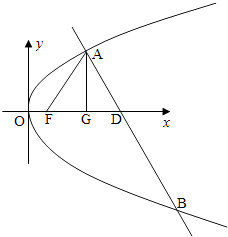

    （1）求C的方程；
    （2）若直线l1∥l，且l1和C有且只有一个公共点E，
    （ⅰ）证明直线AE过定点，并求出定点坐标；
    （ⅱ）△ABE的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案