
分析 (1)由题意:圆C的圆心在线段MN的垂直平分线上,直线2x-3y+6=0为圆C的一条对称轴.交点即为圆心.可得圆C的方程.设过点(5,1)直线方程,与圆C相切,圆心到直线的距离等于半径,即得直线方程.
(2)过点P(1,0)的直线l与圆C相交,设出直线方程,联立方程组,求出A,B的坐标,求出|PA|•|PB|的关系,化简可得是否为定值.
解答 解:(1)由题意:M(1,4),N(3,2)为圆C上的两点,则斜率KMN=$\frac{4-2}{1-3}=-1$,线段MN的中点为(2,3)则线段MN的垂直平分线的方程为x-y+1=0.
直线2x-3y+6=0与x-y+1=0的交点为(3,4),即圆心为(3,4).半径r=$\sqrt{(3-1)^{2}+(4-4)^{2}}=2$
故得圆C的方程为(x-3)2+(y-4)2=4.
①若切线方程的斜率不存在,则直线方程x=5,恰与圆C相切,符合题意.
②若切线方程的斜率存在,设直线方程为y-1=k1(x-5),即k1x-y-5k1+1=0,
由直线方程,与圆C相切,可得:$\frac{|3{k}_{1}-4-5{k}_{1}+1|}{\sqrt{{{k}_{1}}^{2}+1}}=2$,
解得:k=$-\frac{5}{12}$,
故所求的切线方程为x=5或5x+12y-37=0.
(2)过点P(1,0)的直线l与圆相交,可知直线l的斜率存在,设直线l的方程为k2x-y-k2=0,
由$\left\{\begin{array}{l}{{k}_{2}x-y-{k}_{2}=0}\\{x+2y+2=0}\end{array}\right.$,解得B($\frac{2{k}_{2}-2}{2{k}_{2}+1}$,-$\frac{3{k}_{2}}{2{k}_{2}+1}$),
由直线AC与直线l垂直,由$\left\{\begin{array}{l}{y={k}_{2}x-{k}_{2}}\\{y-4=-\frac{1}{{k}_{2}}(x-3)}\end{array}\right.$,解得A($\frac{{{k}_{2}}^{2}+{4}_{2}k+3}{1+{{k}_{2}}^{2}}$,$\frac{4{{k}_{2}}^{2}+2{k}_{2}}{1+{{k}_{2}}^{2}}$),
所以|AP|•|PB|=$\sqrt{(\frac{{{k}_{2}}^{2}+4{k}_{2}+3}{1+{{k}_{2}}^{2}}-1)^{2}+(\frac{4{{k}_{2}}^{2}+2{k}_{2}}{1+{{k}_{2}}^{2}})^{2}}$•$\sqrt{(\frac{2{k}_{2}-2}{2{k}_{2}+1}-1)^{2}+(-\frac{3{k}_{2}}{2{k}_{2}+1})^{2}}$=$\frac{2|2{k}_{2}+1|}{1+{{k}_{2}}^{2}}•\sqrt{1+{{k}_{2}}^{2}}•\frac{3\sqrt{1+{{k}_{2}}^{2}}}{|2{k}_{2}+1|}$=6为定值.
故得|PA|•|PB|是定值6.
点评 本题考查了直线圆的位置关系的,圆的方程的求法以及化简计算的能力,综合性强.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {2,4,5,6,7,8} | C. | {5,6,7} | D. | {4,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
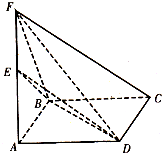 在四棱锥F-ABCD中,底面ABCD是平行四边形,AB=4,AD=8,∠BAD=60°,FA⊥平面ABCD且FA=12,点E在FA上,FC∥平面BED,
在四棱锥F-ABCD中,底面ABCD是平行四边形,AB=4,AD=8,∠BAD=60°,FA⊥平面ABCD且FA=12,点E在FA上,FC∥平面BED,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com