
(本小题满分12分)上海某玩具厂生产 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为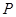 元,且
元,且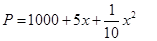 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为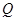 元,其中
元,其中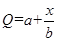
 ,
,
(1)问:该玩具厂生产多少套“海宝”时,使得每套所需成本费用最少?
(2)若生产出的“海宝”能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求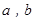 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某售报亭每天以每份0.4元的价格从报社购进若干份报纸,然后以每份1元的价格出售,如果当天卖不完,剩下的报纸以每份0.1元的价格卖给废品收购站.
(Ⅰ)若售报亭一天购进270份报纸,求当天的利润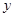 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份,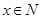 )的函数解析式.
)的函数解析式.
(Ⅱ)售报亭记录了100天报纸的日需求量(单位:份),整理得下表:
日需求量 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
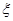 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求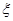 的数学期望;
的数学期望;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时8元,而其他与速度无关的费用是每小时128元.
(1)求轮船航行一小时的总费用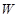 与它的航行速度
与它的航行速度 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;
(2)问此轮船以多大的速度航行时,能使每公里的总费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)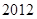 年中秋、国庆长假期间,由于国家实行
年中秋、国庆长假期间,由于国家实行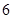 座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午
座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午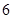 点到中午
点到中午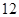 点,车辆通过该收费站的用时
点,车辆通过该收费站的用时 (分钟)与车辆到达该收费站的时刻
(分钟)与车辆到达该收费站的时刻 之间的函数关系式可近似地用以下函数给出:
之间的函数关系式可近似地用以下函数给出:
y=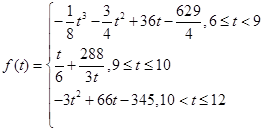
求从上午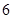 点到中午
点到中午 点,通过该收费站用时最多的时刻。
点,通过该收费站用时最多的时刻。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)
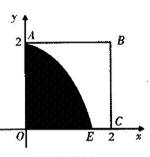
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路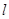 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数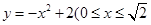 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为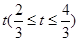 .
.
(1)当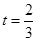 时,求直路
时,求直路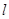 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路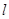 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是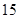 元,销售价是
元,销售价是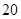 元,月平均销售
元,月平均销售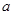 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为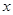
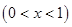 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为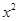 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是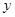 (元).
(元).
(1)写出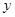 与
与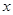 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某服装厂某年1月份、2月份、3月份分别生产某名牌衣服1万件、 万件、
万件、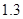 万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量
万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量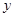 与月份
与月份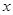 的关系,模拟函数可选用函数
的关系,模拟函数可选用函数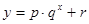 (其中
(其中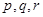 为常数)或二次函数。又已知当年4月份该产品的产量为
为常数)或二次函数。又已知当年4月份该产品的产量为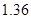 万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com