
(本小题满分12分)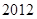 年中秋、国庆长假期间,由于国家实行
年中秋、国庆长假期间,由于国家实行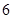 座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午
座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午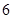 点到中午
点到中午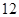 点,车辆通过该收费站的用时
点,车辆通过该收费站的用时 (分钟)与车辆到达该收费站的时刻
(分钟)与车辆到达该收费站的时刻 之间的函数关系式可近似地用以下函数给出:
之间的函数关系式可近似地用以下函数给出:
y=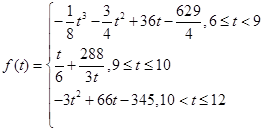
求从上午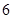 点到中午
点到中午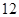 点,通过该收费站用时最多的时刻。
点,通过该收费站用时最多的时刻。
科目:高中数学 来源: 题型:解答题
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1的一条折线表示;西红柿的种植成本与上市时间的关系用图2的抛物线表示.
(1)写出图1表示的市场售价与时间的函数关系式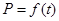 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式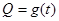 .
.
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/百千克,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知二次函数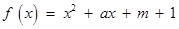 ,关于
,关于 的不等式
的不等式 的解集为
的解集为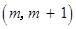 ,其中
,其中 为非零常数.设
为非零常数.设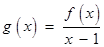 .
.
(1)求 的值;
的值;
(2)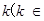 R
R 如何取值时,函数
如何取值时,函数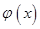
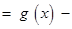
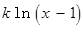 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若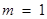 ,且
,且
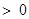 ,求证:
,求证: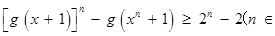 N
N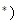
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)某企业拟投资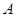 、
、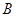 两个项目,预计投资
两个项目,预计投资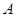 项目
项目 万元可获得利润
万元可获得利润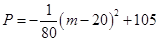
万元;投资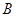 项目
项目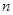 万元可获得利润
万元可获得利润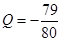
 万元.若该企业用40
万元.若该企业用40
万元来投资这两个项目,则分别投资多少万元能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.已知凹槽的强度与横截面的面积成正比,比例系数为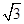 ,设AB=2x,BC=y.
,设AB=2x,BC=y.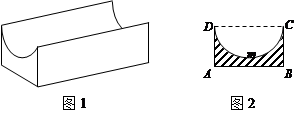
(1)写出y关于x函数表达式,并指出x的取值范围;
(2)求当x取何值时,凹槽的强度最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
(本小题满分12分)某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为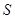 平方米.
平方米.
(1)分别写出用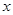 表示
表示 和用
和用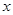 表示
表示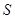 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)上海某玩具厂生产 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为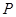 元,且
元,且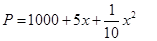 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为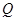 元,其中
元,其中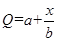
 ,
,
(1)问:该玩具厂生产多少套“海宝”时,使得每套所需成本费用最少?
(2)若生产出的“海宝”能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求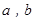 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com