练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    把函数y=f(x)在x=a及x=b之间的一段图像近似地看作直线，设a≤c≤b，证明f(c)的近似值是：f(a)+［f(b)-f(a)］.

    证明:如图4,依题意,点M、N的坐标分别为(a,f(a))、(b,f(b)),

    图4

    所以直线MN的方程为y-f(a)=(x-a),其中a≤x≤b.

    因为a≤c≤b,所以当x=c时,有y=f(a)+(c-a).

    因为在x=a,x=b之间的一段图像可以近似地看作直线,

    所以有f(c)≈f(a)+(c-a),

    即f(c)的近似值为f(a)+［f(b)-f(a)］.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：013

    如图所示，把函数y=f(x)在x∈[a，b]之间的一段图像近似地看作线段。设a≤c≤b，则f(c)的近似值可以表示为（    ）

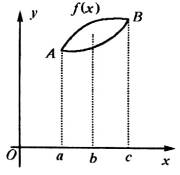
    A．

    B．

    C．

    D．　　　　　　　　　　　　

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

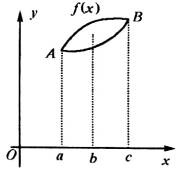
    如图所示，把函数y=f(x)在x∈[a，b]之间的一段图像近似地看作线段。设a≤c≤b，则f(c)的近似值可以表示为（    ）

    A．

    B．

    C．

    D．　　　　　　　　　　　　

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分13分）

    已知函数f (x) = 2cos2x-2sinxcosx + 1．

    （1）设方程f (x) – 1 = 0在(0，)内的两个零点x1，x2，求x1 + x2的值；

    （2）把函数y = f (x)的图象向左平移m (m＞0)个单位使所得函数的图象关于点(0，2)对称，求m的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省福州市高三第五次质量检查数学理卷 题型：解答题

    已知函数f (x) = 2cos2x-2sinxcosx + 1．

    （1）设方程f (x) – 1 = 0在(0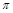，)内的两个零点x1，x2，求x1 + x2的值；

    （2）把函数y = f (x)的图象向左平移m (m＞0)个单位使所得函数的图象关于点(0，2)对称，求m的最小值．

     

     

    查看答案和解析>>

    同步练习册答案