
| A. | 若两条直线和同一个平面所成的角相等,则这两条直线平行 | |
| B. | 若一个平面内有无数个点到另一个平面的距离相等,则这两个平面平行 | |
| C. | 若一条直线平行于两个相交平面的交线,则这条直线与这两个平面都平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行或相交 |
分析 作出正方体,对ABCD四个选项逐一结合图形分析即可得到答案.
解答 解:作图如下: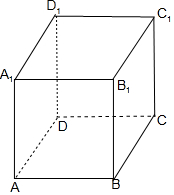
A.若两条直线和同一个平面所成的角相等,则这两条直线相交(如相交直线A1D1与A1B1与底面ABCD均成0°角)、平行(如A1D1与B1C1与底面ABCD均成0°角,但A1D1∥B1C1)或异面(AD1与B1C均与底面ABCD成45°角,但二者为异面直线),故A错误;
B.若一个平面内有无数个点到另一个平面的距离相等,则这两个平面平行(如图中上下两个底面)或相交(平面DCC1DI上有无数个点到平面ABCD的距离相等,但平面DCC1DI与底面ABCD相交),故B错误;
C.若一条直线平行于两个相交平面的交线,则这条直线与这两个平面都平行(如平面DCC1DI∩平面ABCD=CD,A1B1∥CD,且A1B1∥平面DCC1DI,A1B1∥平面ABCD)或这条直线在其中一平面内(如平面DCC1DI∩平面ABCD=CD,C1D1∥CD,但C1D1?平面DCC1DI,故C错误;
D.若两个平面都垂直于第三个平面,则这两个平面平行(如图中上下两个底面平行,均与平面A1ABB1垂直)或相交(如图中平面ADD1A1与平面DCC1D1均与底面垂直,但二者相交),故D正确.
故选:D.
点评 本题考查空间中直线与直线、直线与平面、平面与平面的位置关系,考查空间想象能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 43π | B. | 17π | C. | 34π | D. | $\frac{17π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{2}}}{2}]$ | B. | $[\frac{1}{2},\frac{{\sqrt{2}}}{2}]$ | C. | $(\frac{1}{2},\frac{{\sqrt{2}}}{2}]$ | D. | $(1,\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{4}$ | C. | 4$\sqrt{2}$ | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com