
分析 (1)利用两角和与差的正弦公式,结合特殊角的三角函数值,化简求值;
(2)利用三角恒等变换,化简求值即可.
解答 解:∵sin(α+$\frac{π}{4}$)+sin(α-$\frac{π}{4}$)=$\frac{\sqrt{2}}{3}$,
∴(sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$)+(sinαcos$\frac{π}{4}$-cosαsin$\frac{π}{4}$)=$\frac{\sqrt{2}}{3}$,
∴2sinαcos$\frac{π}{4}$=$\frac{\sqrt{2}}{3}$,
∴sinα=$\frac{1}{3}$;
(2)$\frac{{sin(α-\frac{π}{4})}}{1-cos2α-sin2α}$=$\frac{sinαcos\frac{π}{4}-cosαsin\frac{π}{4}}{{2sin}^{2}α-2sinαcosα}$
=$\frac{\frac{\sqrt{2}}{2}(sinα-cosα)}{2sinα(sinα-cosα)}$
=$\frac{\sqrt{2}}{4sinα}$
=$\frac{\sqrt{2}}{4×\frac{1}{3}}$
=$\frac{3\sqrt{2}}{4}$.
点评 本题考查了二倍角公式以及三角恒等变换的应用问题,熟练掌握公式是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | -64 | B. | -32 | C. | $\frac{1}{64}$ | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若两条直线和同一个平面所成的角相等,则这两条直线平行 | |
| B. | 若一个平面内有无数个点到另一个平面的距离相等,则这两个平面平行 | |
| C. | 若一条直线平行于两个相交平面的交线,则这条直线与这两个平面都平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行或相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
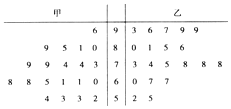 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.| 甲班(A方式) | 乙班(B方式) | 总 计 | |
| 成绩优秀 | 1 | 5 | 6 |
| 成绩不优秀 | 19 | 15 | 34 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},1]$ | B. | $(0,\frac{2}{3})$ | C. | $(\frac{2}{3},1]$ | D. | $(\frac{1}{2},\frac{2}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com