练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在直角梯形ABCD中，AD∥BC，∠A=90°，AB=AD=1，BC=2，E是CD的中点， 则       .


     -1；   


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数（）的最小正周期为.

    （Ⅰ）求的值及函数的单调递增区间；

    （Ⅱ）当时，求函数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：

    空气质量指数

    0-50

    51-100

    101-150

    151-200

    201-300

    300以上

    空气质量等级

    1级优

    2级良

    3级轻度污染

    4级中度污染

    5级重度污染

    6级严重污染

    由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如下：

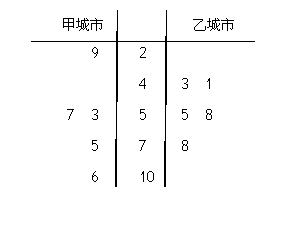
    （Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；

    （Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；

    （Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．

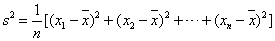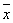    (注：，其中为数据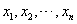的平均数.)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设满足以下两个条件的有穷数列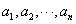为n（n=2,3,4,…,）阶“期待数列”：

    ①    ；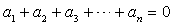

    ②    .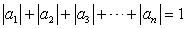

    （Ⅰ）分别写出一个单调递增的3阶和4阶“期待数列”；

    （Ⅱ）若某2013阶“期待数列”是等差数列，求该数列的通项公式；

    （Ⅲ）记n阶“期待数列”的前k项和为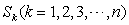，试证：.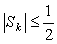

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果函数y=f(x)图像上任意一点的坐标（x,y）都满足方程 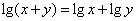，那么正确的选项是

    (A)  y=f(x)是区间（0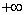，）上的减函数，且x+y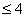

    (B)  y=f(x)是区间（1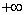，）上的增函数，且x+y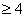

    (C)  y=f(x)是区间（1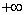，）上的减函数，且x+y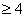

    (D)  y=f(x)是区间（1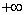，）上的减函数，且x+y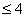

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在一次抽奖活动中，有甲、乙等6人获得抽奖的机会。抽奖规则如下：主办方先从6人中随机抽取两人均获奖1000元，再从余下的4人中随机抽取1人获奖600元，最后还从这4人中随机抽取1人获奖400元。

    （Ⅰ）求甲和乙都不获奖的概率；

    （Ⅱ）设X是甲获奖的金额，求X的分布列和均值。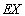

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设，则

    （A）          （B ） 

    （C）          （D）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知，分别是双曲线：的两个焦点，双曲线和圆：的一个交点为，且，那么双曲线的离心率为

    （A）              （B）          （C）              （D）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两个变量x，y之间具有线性相关关系，试验测得(x，y)的四组值分别为(1,2)，(2,4)，(3,5)，(4,7)，则y与x之间的回归直线方程为(　　)

    A．y＝0.8x＋3                           B．y＝－1.2x＋7.5

    C．y＝1.6x＋0.5                         D．y＝1.3x＋1.2

    查看答案和解析>>

    同步练习册答案