
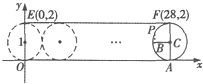
 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于C(28,1)时,线段0P所在直线的方程为
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于C(28,1)时,线段0P所在直线的方程为| 1-cos28 |
| 28-sin28 |
| 1-cos28 |
| 28-sin28 |
| 4-π |
| 4 |
| 4-π |
| 4 |
 |
| PA |
| 28-8π |
| 1 |
| π |
| 2 |
| 17 |
| 2 |
| 17 |
| 2 |
| 17 |
| 2 |
| 1-cos28 |
| 28-sin28 |
| 1-cos28 |
| 28-sin28 |
| ||
| 28×2 |
| 4-π |
| 4 |
| 1-cos28 |
| 28-sin28 |
| 4-π |
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
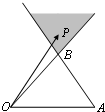 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且| OP |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
查看答案和解析>>
科目:高中数学 来源: 题型:
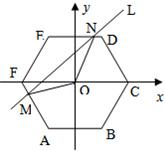 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:

试问:是否存在定点E、F,使|ME|、|MB|、|MF|成等差数列?若存在,求出E、F的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com