
分析 由约束条件作出可行域,求出$\frac{y}{x}$的取值范围,把 $\frac{xy}{{{x^2}+{y^2}}}$化为含$\frac{y}{x}$的代数式后换元,再利用“对勾函数”的单调性求得最值,则答案可求.
解答 解:由约束条件$\left\{\begin{array}{l}x-4y+3≤0\\ x+y-4≤0\\ x≥1\end{array}\right.$作出可行域如图,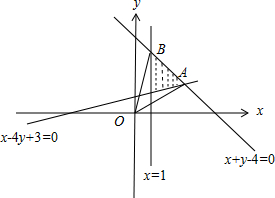
联立$\left\{\begin{array}{l}{x+y-4=0}\\{x-4y+3=0}\end{array}\right.$,解得A($\frac{13}{5},\frac{7}{5}$),
联立$\left\{\begin{array}{l}{x=1}\\{x+y-4=0}\end{array}\right.$,解得B(1,3).
∴$\frac{y}{x}$的取值范围是[$\frac{7}{13},3$].
z=$\frac{xy}{{{x^2}+{y^2}}}$=$\frac{\frac{y}{x}}{1+(\frac{y}{x})^{2}}$,
令$\frac{y}{x}=t$($\frac{7}{13}≤t≤3$),
则z=$\frac{t}{1+{t}^{2}}=\frac{1}{\frac{1}{t}+t}$,当t=1时,z有最大值为$\frac{1}{2}$;
当t=3时,z有最小值为$\frac{3}{10}$.
∴$\frac{xy}{{{x^2}+{y^2}}}$的取值范围为$[\frac{3}{10},\frac{1}{2}]$,
故答案为:$[\frac{3}{10},\frac{1}{2}]$.
点评 本题考查简单的线性规划,考查数形结合的数学思想方法和数学转化思想方法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
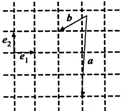 已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.
已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
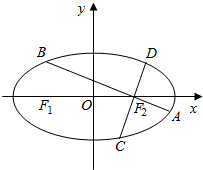 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com