
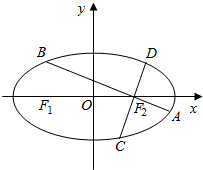
 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.分析 (Ⅰ)通过当直线AB的斜率为0时可知|AB|=2a,$|{CD}|=\frac{{2{b^2}}}{a}$,结合$e=\frac{c}{a}=\frac{1}{2}$,计算即得结论;
(Ⅱ)分别对两条弦的斜率进行讨论,当两条弦中一条斜率为0时、另一条弦的斜率不存在时易得结论;当两条弦斜率均存在且不为0时,通过设直线AB、CD的方程并分别与椭圆方程联立,利用韦达定理及两点间距离公式,可得|AB|+|CD|的表达式,利用换元法及二次函数的性质计算即得结论.
解答 解:(Ⅰ)当直线AB的斜率为0时,直线CD垂直于x轴,
∴|AB|=2a,$|{CD}|=\frac{{2{b^2}}}{a}$,即 $|{AB}|+|{CD}|=2a+\frac{{2{b^2}}}{a}=7$,
∵$e=\frac{c}{a}=\frac{1}{2}$,且a2=b2+c2,解得:$a=2,b=\sqrt{3}$,
所以椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(Ⅱ)①当两条弦中一条斜率为0时,另一条弦的斜率不存在,
由题意可知,|AB|+|CD|=7;
②当两条弦斜率均存在且不为0时,设A(x1,y1),B(x2,y2),
设直线AB的方程为y=k(x-1),则直线CD的方程为$y=-\frac{1}{k}({x-1})$,
将直线AB的方程代入椭圆方程中,并整理得:
(3+4k2)x2-8k2x+4k2-12=0,
∴${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}},{x_1}{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$,
∴$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\frac{{12({{k^2}+1})}}{{3+4{k^2}}}$,
同理,$|{CD}|=\frac{{12({\frac{1}{k^2}+1})}}{{3+\frac{4}{k^2}}}=\frac{{12({{k^2}+1})}}{{3{k^2}+4}}$,
∴$|{AB}|+|{CD}|=\frac{{12({{k^2}+1})}}{{3+4{k^2}}}+\frac{{12({{k^2}+1})}}{{3{k^2}+4}}=\frac{{84{{({{k^2}+1})}^2}}}{{({3+4{k^2}})({3{k^2}+4})}}$,
令t=k2+1,则t>1,
∴$|{AB}|+|{CD}|=\frac{{84{t^2}}}{{({4t-1})({3t+1})}}=\frac{{84{t^2}}}{{12{t^2}+t-1}}=\frac{84}{{-{{({\frac{1}{t}-\frac{1}{2}})}^2}+\frac{49}{4}}}$,
∵t>1,∴$0<\frac{1}{t}<1$,
∴$12<-{({\frac{1}{t}-\frac{1}{2}})^2}+\frac{49}{4}≤\frac{49}{4}$,∴$\frac{4}{49}≤\frac{1}{{-{{({\frac{1}{t}-\frac{1}{2}})}^2}+\frac{49}{4}}}<\frac{1}{12}$,
∴$\frac{48}{7}≤\frac{84}{{-{{({\frac{1}{t}-\frac{1}{2}})}^2}+\frac{49}{4}}}<7$,∴$\frac{48}{7}≤|{AB}|+|{CD}|<7$,
综合①②可知,|AB|+|CD|的取值范围为:[$\frac{48}{7}$,7].
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
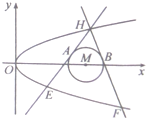 已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.
已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{2}]$ | B. | $[\sqrt{2},+∞)$ | C. | $(1,\sqrt{3}]$ | D. | $[\sqrt{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 11? | B. | 12? | C. | 13? | D. | 14? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com