
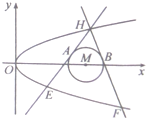
 已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.
已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.分析 (1)利用点M到抛物线准线的距离为$\frac{17}{4}$,可得p=$\frac{1}{2}$,从而可求抛物线C的方程;
(2)根据当∠AHB的角平分线垂直x轴时,点H(4,2),可得kHE=-kHF,设E(x1,y1),F(x2,y2),可得y1+y2=-2yH=-4,从而可求直线EF的斜率;
(3)求以H为圆心、HA为半径的圆方程与⊙M方程相减可得公共弦所在直线AB的方程,当x=0时,直线AB在y轴上的截距t=4m-$\frac{15}{m}$(m≥1),再利用导数法,即可求得t的最小值.
解答 解:(1)∵点M到抛物线准线的距离为4+$\frac{p}{2}$=$\frac{17}{4}$,
∴p=$\frac{1}{2}$,∴抛物线C的方程为y2=x;
(2)∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=-kHF,
设E(x1,y1),F(x2,y2),则$\frac{{y}_{H}-{y}_{1}}{{x}_{H}-{x}_{1}}$=-$\frac{{y}_{H}-{y}_{2}}{{x}_{H}-{x}_{2}}$,
∴$\frac{{y}_{H}-{y}_{1}}{{{y}_{H}}^{2}-{{y}_{1}}^{2}}$=-$\frac{{y}_{H}-{y}_{2}}{{{y}_{H}}^{2}-{{y}_{2}}^{2}}$,∴y1+y2=-2yH=-4.
∴kEF=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{{y}_{2}-{y}_{1}}{{{y}_{2}}^{2}-{{y}_{1}}^{2}}$=$\frac{1}{{{y}_{1}+y}_{2}}$=-$\frac{1}{4}$;
(3)设点H(m2,m)(m≥1),则HM2=m4-7m2+16,
∴HA2=HM2-AM2=m4-7m2+15.
以H为圆心,HA为半径的圆方程为(x-m2)2+(y-m)2=m4-7m2+15,①
⊙M方程:(x-4)2+y2=1. ②
①-②得:直线AB的方程为(2x-m2-4)(4-m2)-(2y-m)m=m4-7m2+14,
当x=0时,直线AB在y轴上的截距t=4m-$\frac{15}{m}$(m≥1),
∵t′=4+$\frac{15}{{m}^{2}}$,∴t关于m的函数在[1,+∞)上单调递增,
∴当m=1时,tmin=-11.
点评 本题以抛物线与圆的方程为载体,考查抛物线的标准方程,考查直线方程,同时考查利用导数法解决函数的最值问题,综合性较强,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
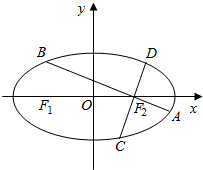 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [-1,3] | C. | [3,5] | D. | [5,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com