
分析 利用数学归纳法证明,只要利用归纳假设证明:当n=k+1时,左边=1+3+5+…+(2k-3)+(2k-1)+(2k+1)+(2k-1)+(2k-3)+…+5+3+1=2k2+2k+1=2(k+1)2-2(k+1)+1=右边即可.
解答 证明:利用数学归纳法证明:
(1)当n=1时,左边=1=右边,此时等式成立;
(2)假设当n=k∈N*时,1+3+5+…+(2k-3)+(2k-1)+(2k-3)+…+5+3+1=2k2-2k+1(k∈N*)成立.
则当n=k+1时,左边=1+3+5+…+(2k-3)+(2k-1)+(2k+1)+(2k-1)+(2k-3)+…+5+3+1=2k2-2k+1+(2k+1)+(2k-1)=2k2+2k+1=2(k+1)2-2(k+1)+1=右边,
∴当n=k+1时,等式成立.
综上可得:对于?n∈N*,1+3+5+…+(2n-3)+(2n-1)+(2n-3)+…+5+3+1=2n2-2n+1成立.
点评 本题考查了数学归纳法证明等式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {0,1} | C. | {0,1,2} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
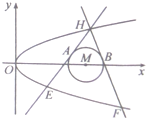 已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.
已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
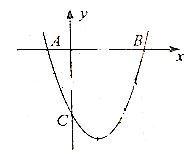 如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.
如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com