
分析 (1)先求导,判断函数f(x)在区间[${e}^{\frac{1}{4}}$,e]上的单调性,再求出端点值,比较即可得到最值;
(2)先化简,再求导,构造h(x)=2lnx-1+$\frac{2}{\sqrt{e}x}$,利用导数判断出h(x)≥h(1)>0,再令g′(x)=0,求出函数的单调区间.
(3)先化简,在求导,构造t(x)=2lnx-1+$\frac{2m}{x}$,再求导,从而可判断0<a<m,b=2m<1,c>1,而证明.
解答 解:(1)∵f(x)=$\frac{{x}^{2}}{lnx}$,x∈[${e}^{\frac{1}{4}}$,e]上,
∴f′(x)=$\frac{x(2lnx-1)}{l{n}^{2}x}$,
令f′(x)=0,解得x=$\sqrt{e}$,
当f′(x)>0时,即$\sqrt{e}$<x≤e时,函数f(x)单调递增,
当f′(x)<0时,即${e}^{\frac{1}{4}}$≤x<$\sqrt{e}$时,函数f(x)单调递减,
当x=$\sqrt{e}$时,函数f(x)有极小值,也是最小值,即f(x)min=f($\sqrt{e}$)=2e,
f(e)=e2>f(${e}^{\frac{1}{4}}$)=4$\sqrt{e}$,
∴f(x)max=f(e)=e2;
(2)g(x)=$\frac{{x}^{2}+4(\frac{1}{\sqrt{e}})^{2}-4\frac{1}{\sqrt{e}}x}{lnx}$=$\frac{(x-\frac{2}{\sqrt{e}})^{2}}{lnx}$,x>0,且x≠1,
∴g′(x)=$\frac{(x-\frac{2}{\sqrt{e}})(2lnx-1+\frac{2}{\sqrt{e}x})}{l{n}^{2}x}$,
令h(x)=2lnx-1+$\frac{2}{\sqrt{e}x}$,
∴h′(x)=$\frac{2}{x}$-$\frac{2}{\sqrt{e}{x}^{2}}$=$\frac{2(x-1)}{\sqrt{e}{x}^{2}}$,
令h′(x)=0,解得x=1,
∴h(x)在(0,1)上单调递减,再(1,+∞)上单调递增,
∴h(x)≥h(1)=$\frac{2}{\sqrt{e}}$-1>0,
令g′(x)=0,解得x=$\frac{2\sqrt{e}}{e}$>1
当g′(x)>0时,x>$\frac{2\sqrt{e}}{e}$时,函数g(x)单调递增,
当g′(x)<0时,即0<x<1,和1<x<$\frac{2\sqrt{e}}{e}$时,函数g(x)单调递减,
综上所述g(x)在($\frac{2\sqrt{e}}{e}$+∞)单调递增,在(0,1)和(1,$\frac{2\sqrt{e}}{e}$)单调递减.
(3)G(x)=G(x)=f(x)+$\frac{4{m}^{2}-4mx}{lnx}$=$\frac{(x-2m)^{2}}{lnx}$,
∴G′(x)=$\frac{(x-2m)(2lnx-1+\frac{2m}{x})}{l{n}^{2}x}$,
令t(x)=2lnx-1+$\frac{2m}{x}$,
则t′(x)=$\frac{2(x-m)}{{x}^{2}}$
故t(x)在(0,m)上单调递减,在(m,1)和(1,+∞)上单调递增;
而函数G(x)有三个极值点为a,b,c,
则t(x)=2lnx-1+$\frac{2m}{x}$=0在(0,+∞)上有两个不相等相都不等于2m的根,
且G(x)的一个极值点为2m;
∵m∈(0,$\frac{1}{2}$),tmin(x)=t(m)=2lnm+1<2ln$\frac{1}{2}$+1<0;
t(1)=2ln1+2m-1=2m-1<0;
又∵a<b<c,
∴0<a<m,b=2m<1,c>1;
∴0<2a<b<1<c.
点评 本题考查了导数的综合应用及分类讨论的思想应用,难题在于构造函数以使问题简化,属于难题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
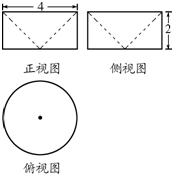
| A. | $\frac{8}{3}$π | B. | $\frac{16}{3}$π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 3+$\sqrt{5}$ | C. | 2$\sqrt{2}$+1 | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com