
| A. | 4$\sqrt{2}$ | B. | 3+$\sqrt{5}$ | C. | 2$\sqrt{2}$+1 | D. | 3+2$\sqrt{2}$ |
分析 设P点的横坐标为x,根据|PF1|=e|PF2|,P在双曲线右支(x≥a),利用双曲线的第二定义,可得x关于e的表达式,进而根据x的范围确定e的范围.
解答 解:设P点的横坐标为x,准线方程为x=±$\frac{{a}^{2}}{c}$,
∵|PF1|=e|PF2|,P在双曲线右支(x≥a),
根据双曲线的第二定义,可得e2(x-$\frac{{a}^{2}}{c}$)=e(x+$\frac{{a}^{2}}{c}$),
∴(e-1)x=$\frac{{a}^{2}}{c}$+a
∵x≥a,
∴$\frac{{a}^{2}}{c}$+a≥(e-1)a,∴e2-2e-1≤0
∵e>1,∴1<e≤2$\sqrt{2}$+1,
则双曲线的离心率的最大值为2$\sqrt{2}$+1.
故选:C.
点评 本题主要考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
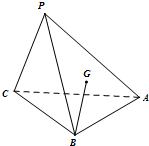 点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.
点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
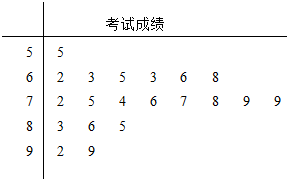
| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )| A. | 100 | B. | 120 | C. | 130 | D. | 390 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com