
分析 由题意跳动10次从原点O到P(2,4),可以分为3类,第一类,向上跳了四次,向右跳了四次,向左跳了两次,第二类,向上跳了五次,向下跳了一次,向右跳了三次,向左跳了一次,第三类,向上跳了六次,向下跳了两次,向右跳了两次,根据分类计数原理即可得到答案.
解答 解:可分三种情况来解.
第一类,向上跳了四次,向右跳了四次,向左跳了两次,故有C104C64=3150种,
第二类,向上跳了五次,向下跳了一次,向右跳了三次,向左跳了一次,故有C105C51C43=5040种,
第三类,向上跳了六次,向下跳了两次,向右跳了两次,故有C106C42=1260种,
根据分类计数原理,共有3150+5040+1260=9450种.
点评 本题考查了分类计数计数原理,关键是分类,属于中档题.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
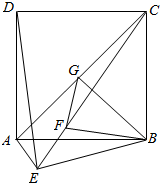 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB=$\sqrt{2}$,F为CE上的点,且BF⊥CE,G为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
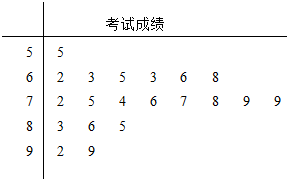
| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com