
分析 找到已知中前三个式子,分析等号右边两项分母的变化规律,即可得到答案.
解答 解:∵已知
$\frac{2}{5}$=$\frac{1}{3}$+$\frac{1}{15}$=$\frac{1}{3}+\frac{1}{3×5}$,
$\frac{2}{7}$=$\frac{1}{4}$+$\frac{1}{28}$=$\frac{1}{4}+\frac{1}{4×7}$,
$\frac{2}{9}$=$\frac{1}{5}$+$\frac{1}{45}$=$\frac{1}{5}+\frac{1}{5×9}$,
…
归纳可得,
$\frac{2}{2n-1}$=$\frac{1}{n}+\frac{1}{n(2n-1)}$(n≥3,且n∈N*)
故答案为:$\frac{1}{n}+\frac{1}{n(2n-1)}$(n≥3,且n∈N*)
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
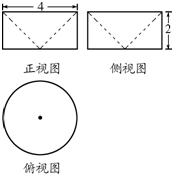
| A. | $\frac{8}{3}$π | B. | $\frac{16}{3}$π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
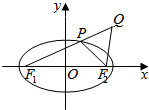 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.
如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com