
分析 (1)由求导公式求出f′(x)代入F(x)化简,由奇函数的性质和条件求出b、c、d,再求出F(x)和F′(x),对t分类讨论并利用导数的符号,求出F(t)的单调性和对应极值;
(2)把t=-26代入F(x)的解析式,由(1)可得F(x)的单调性和极值,再将方程的解转化为图象的交点问题,从而求出实数m的取值范围.
解答 解:(1)由题意得,f′(x)=3x2+2bx+c,
∴F(x)=f(x)-f′(x)=x3+(b-3)x2+(c-2b)x+d-c,
∵F(x)是奇函数,∴b-3=0,且d-c=0,即b=3,d=c.
∴F(x)=x3+(c-6)x,
∵F(1)=t,∴1+(c-6)=t,则d=c=t+5,
则F(x)=x3+(t-1)x,即F′(x)=3x2+(t-1),
①当t≥1时,F′(x)≥0,则F(x)在(-∞,+∞)上递增,无极值;
②当t<1时,由F′(x)=0得,x=$-\sqrt{\frac{1-t}{3}}$或$\sqrt{\frac{1-t}{3}}$,
当x∈($-\sqrt{\frac{1-t}{3}}$,$\sqrt{\frac{1-t}{3}}$)时,F′(x)<0;当x∈(-∞,$-\sqrt{\frac{1-t}{3}}$)或($\sqrt{\frac{1-t}{3}}$,+∞)F′(x)>0,
所以F(x)在($-\sqrt{\frac{1-t}{3}}$,$\sqrt{\frac{1-t}{3}}$)上递减,在(-∞,$-\sqrt{\frac{1-t}{3}}$)、($\sqrt{\frac{1-t}{3}}$,+∞)上递增,
则函数F(x)的极大值是$F(-\sqrt{\frac{1-t}{3}})=-(\frac{1-t}{3})^{3}+(t-1)×(-\sqrt{\frac{1-t}{3}})=\frac{2}{9}(1-t)\sqrt{3(1-t)}$,
函数F(x)的极小值是$F(\sqrt{\frac{1-t}{3}})=-\frac{2}{9}(1-t)\sqrt{3(1-t)}$;
(2)当t=-26时,F(x)=x3-27x,
由(1)可知,F(x)在(-3,3)上单调递减,在(-∞,-3)、(3,+∞)上单调递增,
所以函数F(x)的极大值是F(-3)=54,函数F(x)的极小值是F(3)=-54,
因为方程F(x)=m有三个不同的实数解,
所以函数y=F(x)和y=m的图象有三个不同的交点,
故实数m的取值范围是(-54,54).
点评 本题考查了函数的导数与函数的单调性、极值、最值的关系,方程的根转化问题,以及分类讨论思想、转化思想,属于中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
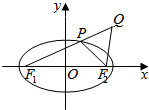 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | a≤-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com