
分析 设A(x1,y1),依题意可求得抛物线y2=x的焦点F($\frac{1}{4}$,0)与准线方程x=-$\frac{1}{4}$,利用抛物线的定义,将|AF|转化为点A到其准线的距离,通过解方程组即可求得|FA|的最大值,从而可得|AF|的取值范围.
解答 解:设A(x1,y1),依题意,抛物线y2=x的焦点F($\frac{1}{4}$,0),准线方程为x=-$\frac{1}{4}$,
由抛物线的定义知,|FA|=x1+$\frac{1}{4}$
当θ=180°时,x1=0,|FA|=$\frac{1}{4}$,此时直线和抛物线只有一个交点,与题意不符;
当θ=45°时,|FA|最大,此时直线FA的方程为:y=x-$\frac{1}{4}$,
由$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=x-\frac{1}{4}}\end{array}\right.$得x2-$\frac{3}{2}$x+$\frac{1}{16}$=0,
解得x=$\frac{3}{4}+\frac{\sqrt{2}}{2}$或x=$\frac{3}{4}$-$\frac{\sqrt{2}}{2}$(舍).
∴|FA|max=$\frac{3}{4}+\frac{\sqrt{2}}{2}$+$\frac{1}{4}$=1+$\frac{\sqrt{2}}{2}$.
∴|AF|的取值范围是($\frac{1}{4}$,1+$\frac{\sqrt{2}}{2}$].
故答案为:($\frac{1}{4}$,1+$\frac{\sqrt{2}}{2}$].
点评 本题考查抛物线的简单性质,考查方程思想与等价转化思想,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
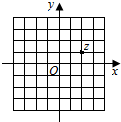 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
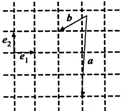 已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.
已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
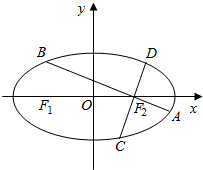 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com