
已知二次函数f(x)=ax2+bx+c(a>0)的图象与x轴有两个不同的交点,若f(c)=0,且0<x<c时,f(x)>0.
(1)证明: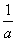 是函数f(x)的一个零点;
是函数f(x)的一个零点;
(2)试用反证法证明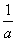 >c.
>c.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}满足b3=3,b5=9.
(1)分别求数列{an},{bn}的通项公式;
(2)设cn=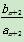 (n∈N*),求证:cn+1<cn≤
(n∈N*),求证:cn+1<cn≤ .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列推理是归纳推理的是( )
A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆
B.由a1=1,an=3n-1,求出S1,S2,S3猜想出数列的前n项和Sn的表达式
C.由圆x2+y2=r2的面积πr2,猜想出椭圆 +
+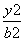 =1的面积S=πab
=1的面积S=πab
D.科学家利用鱼的沉浮原理制造潜艇
查看答案和解析>>
科目:高中数学 来源: 题型:
若{an}是等差数列,m,n,p是互不相等的正整数,则有:(m-n)ap+(n-p)am+(p-m)an=0,类比上述性质,相应地,对等比数列{bn}有________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com