
从某校高三上学期期末数学考试成绩中,随机抽取了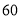 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下:
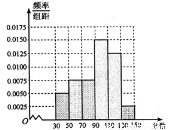
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在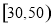 和
和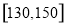 的学生中共抽取
的学生中共抽取 人,该
人,该 人中成绩在
人中成绩在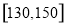 的有几人?
的有几人?
(3)在(2)中抽取的 人中,随机抽取
人中,随机抽取 人,求分数在
人,求分数在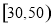 和
和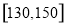 各
各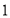 人的概率.
人的概率.
(1)该校高三学生本次数学考试的平均分为92分;(2)抽取的3人中分数在[130,150]的人有1人;(3)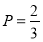 .
.
【解析】
试题分析:(1)根据由频率分布直方图,计算平均值的方法:分别取各个小矩形的宽的中点的横坐标乘以该组的频率,然后将这些乘积相加,即可得到该校高三学生本次数学考试的平均分的估计值;(2)先根据频率分布直方图确定分数在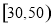 和
和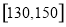 的学生人数各有多少,然后按比例进行抽取,即可得到在[130,150]中应抽取的人数;(3)根据(2)中抽取的3人中,有2人的分数在
的学生人数各有多少,然后按比例进行抽取,即可得到在[130,150]中应抽取的人数;(3)根据(2)中抽取的3人中,有2人的分数在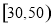 ,有一人的分数在
,有一人的分数在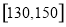 ,从而可确定基本事件总数,然后确定满足要求的基本事件数,根据古典概率的计算公式即可得到分数在
,从而可确定基本事件总数,然后确定满足要求的基本事件数,根据古典概率的计算公式即可得到分数在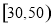 和
和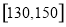 各
各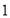 人的概率.
人的概率.
试题解析:(1)由频率分布直方图,得该校高三学生本次数学考试的平均分为
0.0050×20×40+0.0075×20×60+0.0075×20×80+0.0150×20×100
+0.0125×20×120+0.0025×20×140=92. 4分
(2)样本中分数在[30,50)和[130,150]的人数分别为6人和3人
所以抽取的3人中分数在[130,150]的人有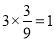 (人) 8分
(人) 8分
(3)由(2)知:抽取的3人中分数在[30,50)的有2人,记为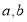
分数在[130,150]的人有1人,记为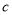 ,从中随机抽取2人
,从中随机抽取2人
总的情形有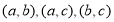 三种.
三种.
而分数在[30,50)和[130,150]各1人的情形有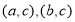 两种
两种
故所求概率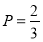 12分.
12分.
考点:1.频率分布直方图;2.平均值的计算;3.分层抽样;4.古典概率.


科目:高中数学 来源:2015届河南省高三上学期第一次月考理科数学试卷(解析版) 题型:解答题
已知函数 (
( 为常数)的图像与
为常数)的图像与 轴交于点
轴交于点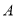 ,曲线
,曲线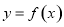 在点
在点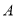 处的切线斜率为
处的切线斜率为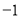 .
.
(1)求 的值及函数
的值及函数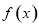 的极值; (2)证明:当
的极值; (2)证明:当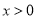 时,
时, .
.
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期第一次月考理科数学试卷(解析版) 题型:选择题
甲乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假定甲每局比赛获胜的概率均为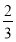 ,则甲以
,则甲以 的比分获胜的概率为( )
的比分获胜的概率为( )
A.  B.
B.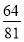 C.
C.  D.
D.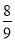
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期第一次月考文科数学试卷(解析版) 题型:解答题
在平面直角坐标系中,以坐标原点为极点,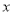 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线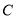 的极坐标方程为
的极坐标方程为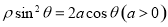 ,过点
,过点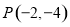 的直线
的直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 与曲线
与曲线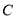 相交于
相交于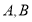 两点.
两点.
(1)写出曲线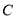 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(2)若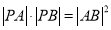 ,求
,求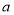 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com