
某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为g(x)万元(总成本=固定成本+生产成本),并且销售收人r(x)满足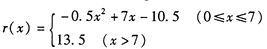 假定该产品产销平衡,根据上述统计规律求:
假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?
(1)大于300台小于1050台; (2) 600台
解析试题分析:(1) 由于销售收入是一个关于产品数量x的一个分段函数,另外计算工厂的盈利需要将销售收入r(x)减去总的成本g(x)万元,所以在两段函数中分别求出盈利大于零的时候产品数量的范围,及可求得结论.
(2)通过二次函数的最值的求法即可得到盈利最大值时对应的产品数x的值,本小题单位的转化也是易错点.
试题解析:依题意得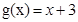 ,设利润函数为
,设利润函数为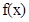 ,则
,则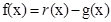 ,
,
所以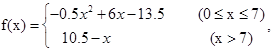 (1)要使工厂有盈利,则有f(x)>0,因为
(1)要使工厂有盈利,则有f(x)>0,因为
f(x)>0?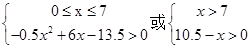 ,
,
⇒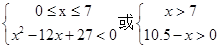 ⇒
⇒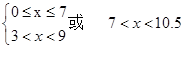
⇒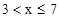 或
或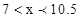 , 即
, 即 .
.
所以要使工厂盈利,产品数量应控制在大于300台小于1050台的范围内
(2)当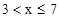 时,
时, 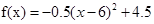
故当x=6时,f(x)有最大值4.5.而当x>7时,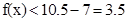 .
.
所以当工厂生产600台产品时,盈利最大.
考点:1.分段函数的应用.2.函数的最值.3.实际问题的构建数学模型解决.


科目:高中数学 来源: 题型:解答题
设f(x)=|lg x|,a,b为实数,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b满足f(a)=f(b)=2f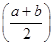 ,
,
求证:a·b=1,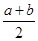 >1.
>1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对定义域分别是Df,Dg的函数y=f(x),y=g(x),规定:函数h(x)=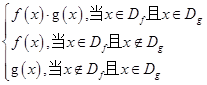
(1)若函数f(x)=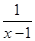 ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;
(2)求问题(1)中函数h(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知两函数f(x)=8x2+16x-k,g(x)=2x3+5x2+4x,其中k为实数.
(1)对任意x∈[-3,3]都有f(x)≤g(x)成立,求k的取值范围.
(2)存在x∈[-3,3]使f(x)≤g(x)成立,求k的取值范围.
(3)对任意x1,x2∈[-3,3]都有f(x1)≤g(x2),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ex,x∈R.
(1)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值;
(2)设x>0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=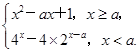
(1)若x<a时,f(x)<1恒成立,求a的取值范围;
(2)若a≥-4时,函数f(x)在实数集R上有最小值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x).当年产量不足80千件时,C(x)= x2+10x(万元);当年产量不小于80千件时,C(x)=51x+
x2+10x(万元);当年产量不小于80千件时,C(x)=51x+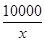 -1 450(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
-1 450(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为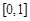 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的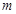 (
(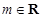 且
且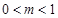 ),存在
),存在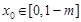 ,使得
,使得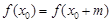 ,则称
,则称 具有性质
具有性质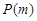 .
.
(1)已知函数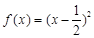 ,
,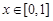 ,判断
,判断 是否具有性质
是否具有性质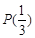 ,并说明理由;
,并说明理由;
(2)已知函数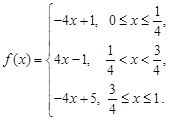 若
若 具有性质
具有性质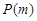 ,求
,求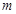 的最大值;
的最大值;
(3)若函数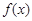 的定义域为
的定义域为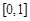 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足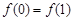 ,
,
求证:对任意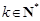 且
且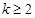 ,函数
,函数 具有性质
具有性质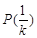 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com