
已知函数 的定义域为
的定义域为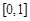 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的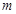 (
(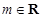 且
且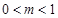 ),存在
),存在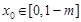 ,使得
,使得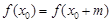 ,则称
,则称 具有性质
具有性质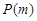 .
.
(1)已知函数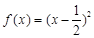 ,
,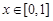 ,判断
,判断 是否具有性质
是否具有性质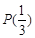 ,并说明理由;
,并说明理由;
(2)已知函数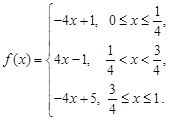 若
若 具有性质
具有性质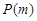 ,求
,求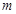 的最大值;
的最大值;
(3)若函数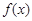 的定义域为
的定义域为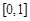 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足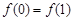 ,
,
求证:对任意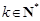 且
且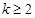 ,函数
,函数 具有性质
具有性质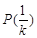 .
.
(1)具有该性质,证明见解析;(2) ;(3)证明见解析.
;(3)证明见解析.
解析

试题分析:(1)创新定义问题,首先要读懂具有性质P(m)的意思, 对于给定的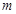 (
(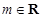 且
且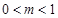 ),存在
),存在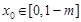 ,使得
,使得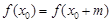 ,按照此定义进行判断,假设具有该性质, 设
,按照此定义进行判断,假设具有该性质, 设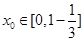 ,令
,令 ,解得
,解得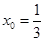
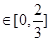 ,满足定义,故具有性质P(3);(2)m在0到1之间,取一半,看是
,满足定义,故具有性质P(3);(2)m在0到1之间,取一半,看是
具有性质P( ),如果有,再判断是否有大于
),如果有,再判断是否有大于 的m,没有的话,最大值就是
的m,没有的话,最大值就是 ;(3)构造函数
;(3)构造函数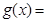
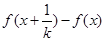 ,则
,则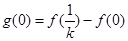 ,
,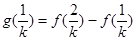 …
…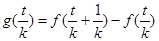 …
…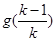 =
=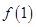 -
-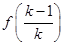 ,相加,有
,相加,有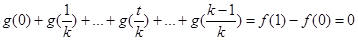 ,分里面有零和没零进行讨论,得到结论.
,分里面有零和没零进行讨论,得到结论.
试题解析:(1)设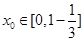 ,即
,即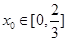
令 , 则
, 则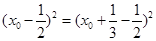
解得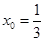
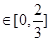 ,
,
所以函数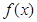 具有性质
具有性质
(2)m的最大值为 .
.
首先当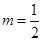 时,取
时,取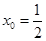 ,
,
则 ,
,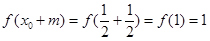 ,
,
所以函数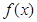 具有性质
具有性质 ,
,
假设存在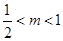 ,使得函数
,使得函数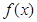 具有性质
具有性质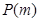 ,
,
则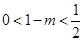 ,
,
当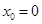 时,
时,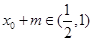 ,
,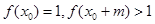 ,
, ,
,
当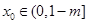 时,
时, ,
,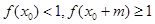 ,
, ,
,
所以不存在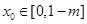 ,使得
,使得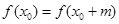 ,
,
故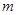 的最大值为
的最大值为 .
.
(3)任取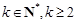 ,
,
设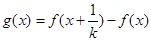 ,其中
,其中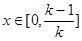 ,
,
则有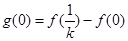 ,
,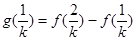 ,
,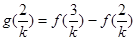 ,
,
……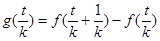 ,
,
……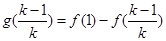 ,
,
以上各式相加得: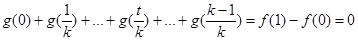 ,
,
当 中有一个为
中有一个为 时,不妨设为
时,不妨设为 ,
,
即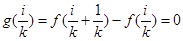 ,
,
则函数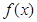 具有性质
具有性质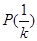 ,
,
当 均不为
均不为 时,由于其和为
时,由于其和为 ,则必然存在正数和负数,
,则必然存在正数和负数,
不妨设 其中
其中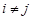


科目:高中数学 来源: 题型:解答题
某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为g(x)万元(总成本=固定成本+生产成本),并且销售收人r(x)满足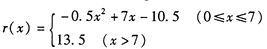 假定该产品产销平衡,根据上述统计规律求:
假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某镇政府为了更好地服务于农民,派调查组到某村考察.据了解,该村有100户农民,且都从事蔬菜种植,平均每户的年收入为3万元.为了调整产业结构,该镇政府决定动员部分农民从事蔬菜加工.据估计,若能动员x(x>0)户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高2x%,而从事蔬菜加工的农民平均每户的年收入将为3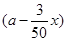 (a>0)万元.
(a>0)万元.
(1)在动员x户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求x的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18-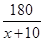 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=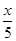 (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我国加入WTO后,根据达成的协议,若干年内某产品关税与市场供应量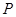 的关系允许近似的满足:
的关系允许近似的满足: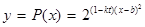 (其中
(其中 为关税的税率,且
为关税的税率,且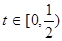 ,
, 为市场价格,
为市场价格,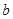 、
、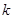 为正常数),当
为正常数),当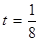 时的市场供应量曲线如图:
时的市场供应量曲线如图: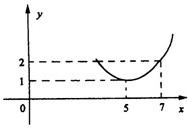
(1)根据图象求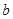 、
、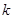 的值;
的值;
(2)若市场需求量为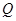 ,它近似满足
,它近似满足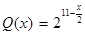 .当
.当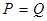 时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数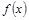 与第x天近似地满足
与第x天近似地满足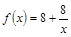 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费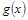 近似地满足
近似地满足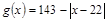 (元).
(元).
(1)求该村的第x天的旅游收入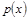 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,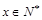 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
方便、快捷、实惠的电动车是很多人的出行工具。可是,随着电动车的普及,它的安全性也越来越受到人们关注。为了出行更安全,交通部门限制电动车的行驶速度为24km/h。若某款电动车正常行驶遇到紧急情况时,紧急刹车时行驶的路程S(单位:m)和时间t(单位:s)的关系为: 。
。
(Ⅰ)求从开始紧急刹车至电动车完全停止所经过的时间;
(Ⅱ)求该款车正常行驶的速度是否在限行范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com